Attention is all you need

Attention is all you need#

import os
os.environ["TOKENIZERS_PARALLELISM"] = "false"

import torch 
from torch import nn

Make sure you have the dataset.py and utils.py in your working directory.

from dataset import PubMedDataset
from utils import train, test, generate

A little bit of history#

In the beginning was the Markov model:

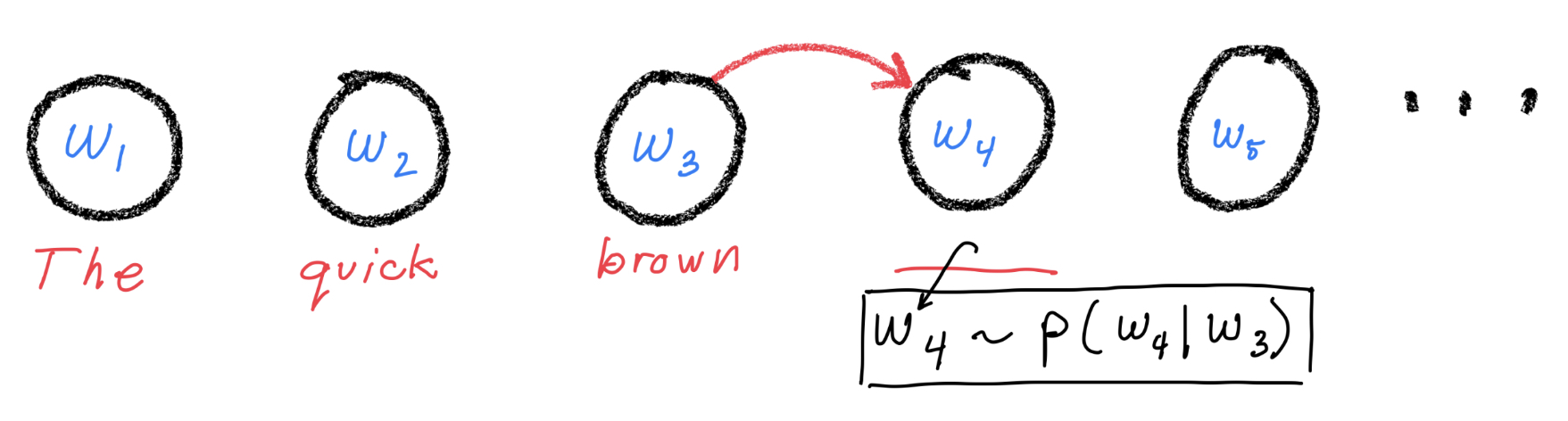
Then came recurrent neural networks (GRU, LSTM, …):

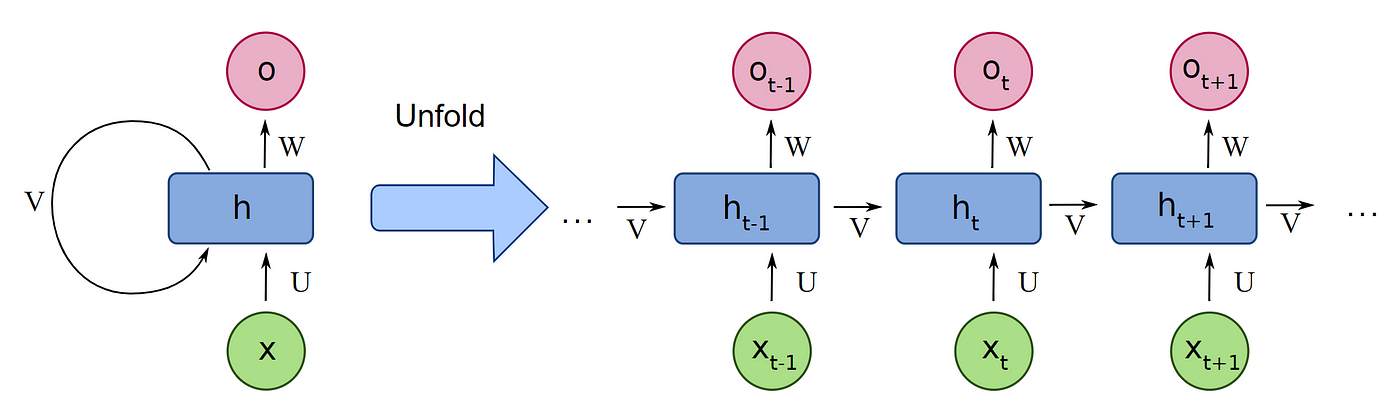
Then came LSTMs with something called attention:

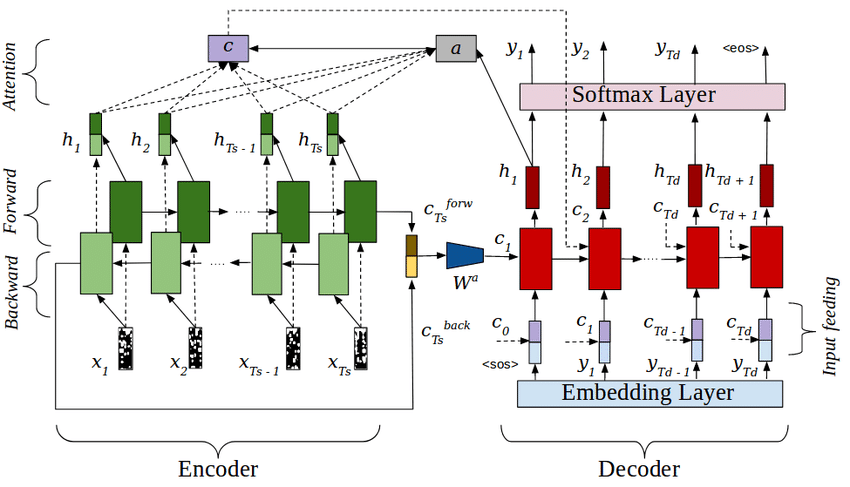
If you are feeling a little overwhelmed by this picture, you are not alone. In fact, exactly that feeling produced the title for the 2017 paper “Attention is all you need”:

And this is what their model architecture looks like:

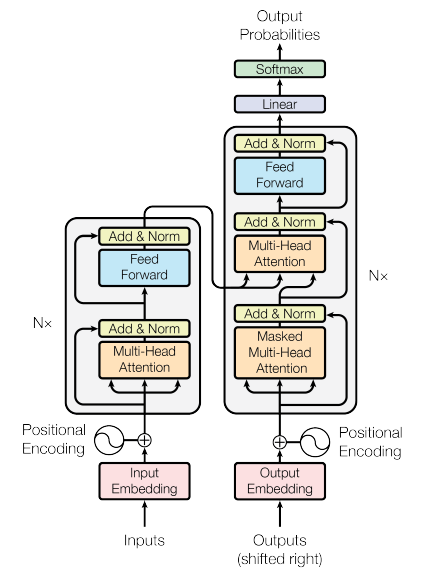
However, they were focused on text translation which benefits from having a separate encoder/decoder. For language modeling, we only need the first half. The picture simplifies to:

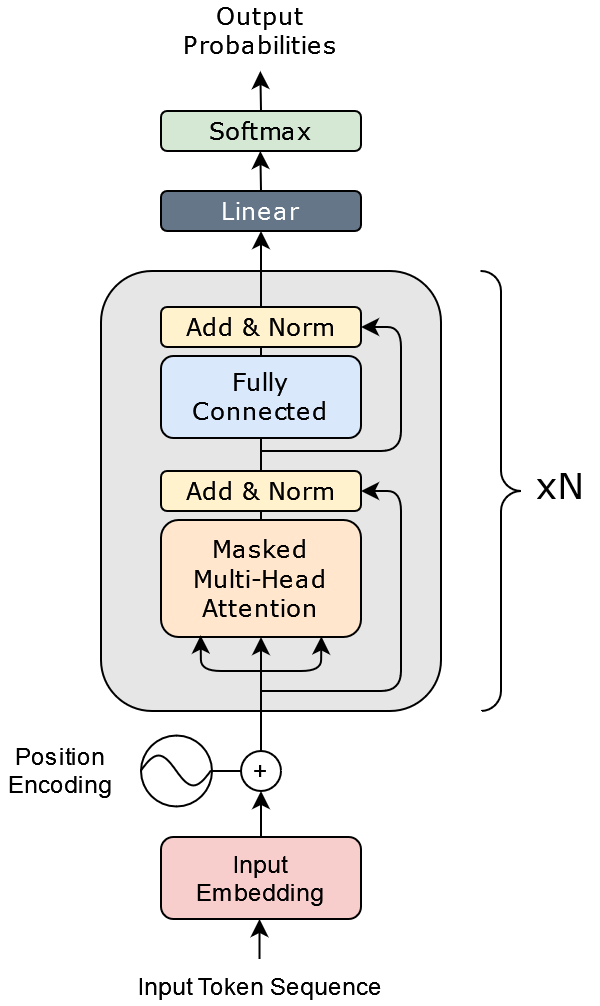
transformer decoder only for language modeling

Now this is starting to be a little less intimidating.

Let’s take stock of what we need to figure out:

Input embedding
Position encoding
The circle plus thing
Masked Multi-Head atttention (MMHA)
Connections going around the MMHA
Add and Norm
Fully Connected
Linear and Softmax

The heart of the transformer is the “Masked Multi-Head attention” step. All of the other operations act at the single-token level.

Masked Multi-Head Attention#

What is attention?#

Attention selects information from a set of entries based on a query. To perform this operation we need to define:

$Q$: the query, represented by a numeric vector. The query specifies what kind of information should be given more attention.
$K$: the keys, also vectors. Each entry in the set has a key. We compare the query with each key to see how much attention the entry should be given.
$V$: the value, also usually a vector. This represents the information associated with each entry that we are retrieving.
$f(Q, K_i) = \alpha_i$: the “comparison” or “compatibility” function. This function compares $Q$ with $K_i$, the key for entry $i$. The function returns the attention logit $\alpha_i$.

The attention scores are computed from the attention logits with the softmax operation: $$ a_i = \frac{\exp{(\alpha_i)}}{\sum_{j=1}^L\exp{(\alpha_j)}} $$ In pytorch, we will simply do a = alpha.softmax(dim=-1).

Let’s work out a simple example.

query = torch.tensor([1., 0.])

values = torch.tensor([0., 
                       1., 
                       0.])

keys = torch.tensor([
    [0.95, 0.05],  # goes with value 0.
    [0.1, 0.9],  # goes with value 1. 
    [0.8, 0.2]    # goes with value 0.
])

# for our comparison function, let's just use the dot product
alpha = keys @ query
print("alpha values:", alpha)

# now compute the normalized attention scores
attn = alpha.softmax(dim=-1)
print("attention values:", attn)

# now use the attention scores to aggregate the values
result = values @ attn
print("Result:", result.item())

Because the query vector was more like the vectors with value 0., our result ended up closer to 0.

Check to see the result when using the query [0., 1.]

Masked Attention for autoregressive language models#

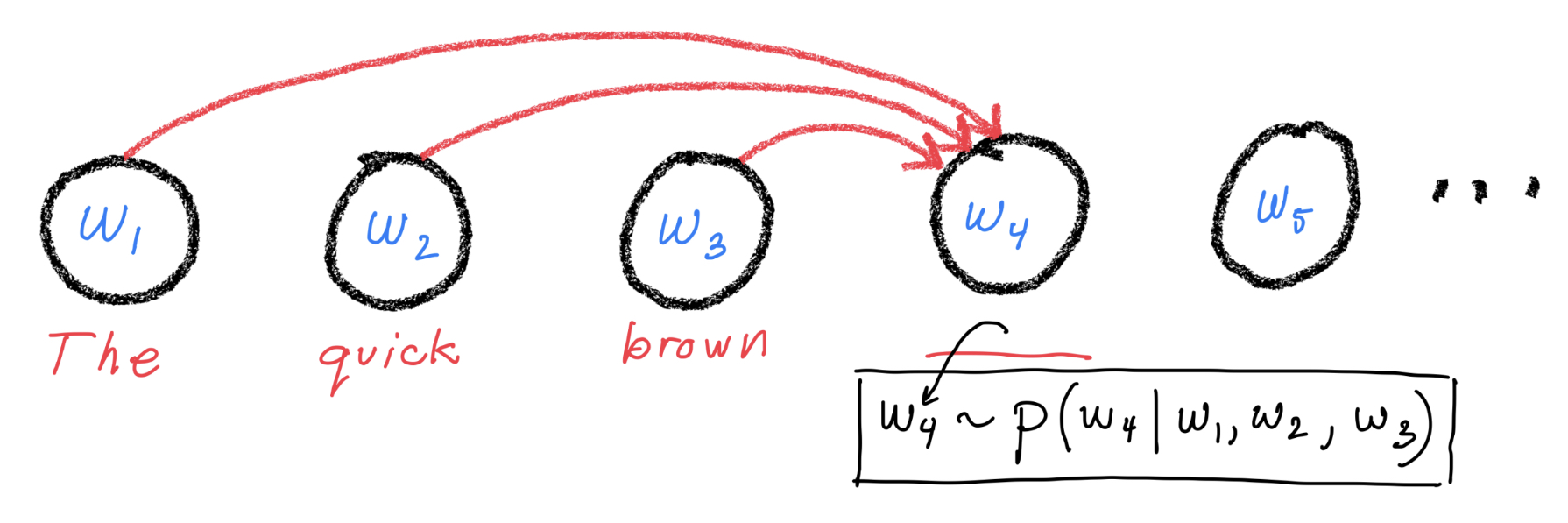
Consider the figure above. In order to make a good prediction for token 4, we need to adaptively combine the information from tokens 1, 2, and 3. Let’s use attention to do this. Here’s how we define Q, K, and, V:

$Q_3 = W_Q h_3$, where $h_3$ is the embedding for token 3 and $W_Q$ is an embed_dim x embed_dim projection matrix.
$K_{i\leq3} = W_K h_i$ where $W_K$ is an embed_dim x embed_dim matrix.
$V_{i\leq3} = W_V h_i$ where $W_V$ is an embed_dim x embed_dim matrix.
$\alpha_{i,3} = \frac{Q_3\cdot K_i}{\sqrt{|Q_3|}}$ where $|Q_3|$ is the number of elements in $Q_3$.

We then use softmax to normalize the attention logits yeilding the attention scores $a_{i,3},\, i\leq3$. The output of the attention block is then $$ h^{(\rm out)}_3 = \sum_{i=1}^3 a_{i,3}V_{i} $$

We’re now ready to implement this in code:

class MaskedAttention(nn.Module):
    def __init__(self, embed_dim, max_tokens, dropout_rate):
        super().__init__()
        self.embed_dim = embed_dim
        self.max_tokens = max_tokens
        self.dropout_rate = dropout_rate
        
        self.scale_factor = embed_dim**-0.5
        
        # q,k,v
        self.query = nn.Linear(embed_dim, embed_dim, bias=False)  # W_Q @ h_i
        self.key = nn.Linear(embed_dim, embed_dim, bias=False)  # W_K @ h_i
        self.value = nn.Linear(embed_dim, embed_dim, bias=False)  # W_V @ h_i
        self.attn_dropout = nn.Dropout(dropout_rate)
        
        # final projection
        self.proj = nn.Sequential(
            nn.Linear(embed_dim, embed_dim, bias=False),
            nn.Dropout(dropout_rate)
        )
        
        # autoregressive mask
        self.register_buffer(
            "ar_mask",
            torch.tril(torch.ones(max_tokens, max_tokens)).unsqueeze(0)
        )  
        # self.ar_mask.shape == (1, L, L)
        # for each batch, we need to select the sub-matrix
        # of size (1, L_batch, L_batch) where L_batch<=L
        # is the sequence length for the batch.

    def forward(self, x):
        # x.shape = (N, L_batch, embed_dim)
        L_batch = x.size(1)
        
        # qkv
        q = self.query(x) # (N, L_batch, embed_dim)
        k = self.key(x) # (N, L_batch, embed_dim)
        v = self.value(x) # (N, L_batch, embed_dim)
        
        # scaled dot-product attention
        # we use einstein summation approach to avoid 
        # complicated reshape then permute operations
        alpha = torch.einsum("Nie,Nje->Nij", q, k) * self.scale_factor
        alpha = self.attn_dropout(alpha)
        # alpha.shape = (N, L_batch, L_batch)
        # the 1st L_batch dim indexes the query token, 
        # the 2nd indexes the key/val token
        
        # autoregressive masking
        mask = self.ar_mask[:, :L_batch, :L_batch] # (1, L_batch, L_batch)
        alpha = alpha.masked_fill(mask==0, float("-inf"))  # why does this work? 
        
        # normalized attention scores
        attn = alpha.softmax(-1)  # N, L_batch, L_batch
        
        # aggregate
        v_agg = torch.einsum("Nij,Nje->Nie", attn, v)
        h_out = self.proj(v_agg)
        
        return h_out # (N, L_batch, embed_dim)

h = torch.randn(3, 462, 32)  # (N, L_batch, embed_dim)
ma = MaskedAttention(embed_dim=32, max_tokens=512, dropout_rate=0.1)
h_out = ma(h)  # expect (3, 462, 32)
h_out.shape

Multi-head Masked Attention#

Now we deal with the “Multi-head” part. The logic here is that using a single attention score to aggregate an entire token embedding may not have enough resolution. Perhaps there are two somewhat independent parts of the embedding that need to be attended to under different circumstances. Multi-head attention addresses this issue. Conceptually, we break up the embedding vector into num_heads smaller embedding vectors and then perform the same attention mechanism as above independently for each sub-vector. We then concatenate the resulting sub-vectors before projecting.

Once we’ve understood the single-head case, the multi-head case is not very difficult to implement. Copy-paste the MaskedAttention class and modify it to incorporate multiple heads.

class MultiHeadMaskedAttention(nn.Module):
    def __init__(self, embed_dim, num_heads, max_tokens, dropout_rate):
        super().__init__()        
        self.embed_dim = embed_dim
        self.num_heads = num_heads
        self.max_tokens = max_tokens
        self.dropout_rate = dropout_rate
        
        assert embed_dim % num_heads == 0, "embed_dim must be divisble by num_heads"
        self.head_dim = embed_dim // num_heads
        self.scale_factor = self.head_dim**-0.5  # now we scale based on head size
        
        # q,k,v
        self.query = nn.Linear(embed_dim, embed_dim, bias=False)  # W_Q @ h_i
        self.key = nn.Linear(embed_dim, embed_dim, bias=False)  # W_K @ h_i
        self.value = nn.Linear(embed_dim, embed_dim, bias=False)  # W_V @ h_i
        self.attn_dropout = nn.Dropout(dropout_rate)
        
        # final projection
        self.proj = nn.Sequential(
            nn.Linear(embed_dim, embed_dim, bias=False),
            nn.Dropout(dropout_rate)
        )
        
        # autoregressive mask
        # we need one extra dimension for the head
        self.register_buffer(
            "ar_mask",
            torch.tril(torch.ones(max_tokens, max_tokens)).unsqueeze(0).unsqueeze(0)
        )  
        # self.ar_mask.shape == (1, 1, L, L)
        # for each batch, we need to select the sub-matrix
        # of size (1, 1, L_batch, L_batch) where L_batch<=L
        # is the sequence length for the batch.

    def forward(self, x):
        # x.shape = (N, L_batch, embed_dim)
        L_batch = x.size(1)
        
        # qkv
        q = self.query(x) # (N, L_batch, num_heads * head_dim)
        k = self.key(x) # (N, L_batch, num_heads * head_dim)
        v = self.value(x) # (N, L_batch, num_heads * head_dim)
        
        # reshape to isolate head embedding
        q,k,v = [vec.view(-1, L_batch, self.num_heads, self.head_dim) for vec in (q,k,v)]
        # vec.shape == (N, L_batch, num_heads, head_dim)
        
        # scaled dot-product attention
        # we use einstein summation approach to avoid 
        # complicated reshape then permute operations
        alpha = torch.einsum("Nihe,Njhe->Nhij", q, k) * self.scale_factor
        alpha = self.attn_dropout(alpha)
        # alpha.shape = (N, num_heads, L_batch, L_batch)
        # the 1st L_batch dim indexes the query token, 
        # the 2nd indexes the key/val token
        
        # autoregressive masking
        mask = self.ar_mask[:, :, :L_batch, :L_batch] # (1, 1, L_batch, L_batch)
        alpha = alpha.masked_fill(mask==0, float("-inf")) 
        
        # normalized attention scores
        attn = alpha.softmax(-1)  # N, num_heads, L_batch, L_batch
        
        # aggregate
        v_agg = torch.einsum("Nhij,Njhe->Nihe", attn, v)  # (N,L_batch,num_heads,head_dim)
        
        # reshape to concat the heads (view won't work)
        v_agg = v_agg.reshape(-1, L_batch, self.embed_dim) # (N, L_batch, embed_dim)
        h_out = self.proj(v_agg)
        
        return h_out # (N, L_batch, embed_dim)

h = torch.randn(3, 462, 32)  # (N, L_batch, embed_dim)
ma = MultiHeadMaskedAttention(embed_dim=32, num_heads=4, max_tokens=512, dropout_rate=0.1)
h_out = ma(h)  # expect (3, 462, 32)
h_out.shape

The Transformer#

Now that we’ve tackled multi-head masked attention, the rest is easy. All other operations act at the individual token level.

class TransformerBlock(nn.Module):
    def __init__(self, embed_dim, num_heads, max_tokens, dropout_rate):
        super().__init__()

        self.lay_norm1 = nn.LayerNorm(embed_dim)
        self.lay_norm2 = nn.LayerNorm(embed_dim)
        self.attn = MultiHeadMaskedAttention(
            embed_dim=embed_dim, 
            num_heads = num_heads,
            max_tokens=max_tokens, 
            dropout_rate=dropout_rate
        )

        self.feed_forward = nn.Sequential(
            nn.Linear(embed_dim, 4*embed_dim),  # the factor of 4 comes from the original GPT paper.
            nn.GELU(),  # like relu but a smooth
            nn.Linear(embed_dim * 4, embed_dim),
            nn.Dropout(dropout_rate)
        )

    def forward(self, x):
        z = self.lay_norm1(x + self.attn(x))
        z = self.lay_norm2(z + self.feed_forward(z))

        return z

class Transformer(nn.Module):
    def __init__(self, vocab_size, embed_dim, num_heads, max_tokens, num_blocks, dropout_rate):
        super().__init__()
        self.vocab_size = vocab_size
        self.embed_dim = embed_dim
        self.num_heads = num_heads
        self.max_tokens = max_tokens
        self.num_blocks = num_blocks
        self.dropout_rate = dropout_rate

        # embeddings
        self.tok_embed = nn.Embedding(vocab_size, embed_dim)
        self.pos_embed = nn.Embedding(max_tokens, embed_dim)

        # sequence of transformer blocks
        self.blocks = nn.Sequential(*[
            TransformerBlock(embed_dim, num_heads, max_tokens, dropout_rate) 
            for i in range(num_blocks)])

        # output linear layer
        self.fout = nn.Linear(embed_dim, vocab_size)

    def forward(self, x):
        # x.shape = (N, L)
        # mask.shape = (N, L)
        L = x.shape[-1]
        pos = torch.arange(0, L, device=x.device, dtype=torch.long)

        # embeddings
        tok_embedding = self.tok_embed(x)  # (N, L, embed_dim)
        pos_embedding = self.pos_embed(pos)  # (L, embed_dim)
        embedding = tok_embedding + pos_embedding  # (N, L, embed_dim)

        # transformer blocks
        h = self.blocks(embedding)

        # output
        logits = self.fout(h)

        return logits
    
    def numpar(self):
        return sum(p.numel() for p in model.parameters() if p.requires_grad)    

# let's test it
dataset = PubMedDataset("/project/rcde/datasets/pubmed/mesh_50k/splits/")
dl_train = dataset.get_dataloader('train', batch_size=3)
batch = next(iter(dl_train))
print(batch.keys())

model = Transformer(
    vocab_size = dataset.tokenizer.vocab_size,
    embed_dim = 64, 
    num_heads = 8,
    max_tokens = 512, 
    num_blocks = 3, 
    dropout_rate = 0.1
)
print(model)
print("Trainable parameters: ", model.numpar())
model(batch['input_ids']).shape

Time to train the model#

# training settings
num_epochs=20
batch_size=64
learning_rate=0.002  # We could get better performance by using a learning rate scheduler

# model settings
embed_dim = 128 # gpt-1 uses 768. We have a much smaller dataset.
num_heads = 4  # gpt uses 12 size 64 heads.
max_tokens = 512 # gpt-1 uses 512
dropout_rate = 0.2 # gpt-1 uses 0.1
num_blocks = 6 # gpt-1 uses 12

# reinitialize dataset for good measure
dataset = PubMedDataset("/project/rcde/datasets/pubmed/mesh_50k/splits/", max_tokens=max_tokens)
vocab_size = dataset.tokenizer.vocab_size

# train/test dataloaders
dl_train = dataset.get_dataloader('train', batch_size=batch_size, num_workers=20)
dl_test = dataset.get_dataloader('test', batch_size=batch_size, num_workers=20)

# reinitialize the model on gpu
model = Transformer(
    vocab_size = dataset.tokenizer.vocab_size,
    embed_dim = embed_dim, 
    num_heads = num_heads,
    max_tokens = max_tokens, 
    num_blocks = num_blocks, 
    dropout_rate = dropout_rate
).to('cuda')

print("Trainable parameters:", model.numpar())

# create the pytorch optimizer
optimizer = torch.optim.AdamW(model.parameters(), lr=learning_rate)

This is going to take a while, and we only have 45k training samples (63MB) and a tiny model (yes 8.7 million is tiny by today’s LLM standards). GPT-3 has about 175 billion parameters and 45 TB of text data. That’s 22 thousand times more model and 700 thousand times more data… Be glad we don’t have to train that! Nevertheless, the basic architecture is very similar to what we wrote down above.

While it trains, try looking at your gpu utilization (for example nvidia-smi -l 3) and cpu utilization (top or htop). Can you identify the bottleneck in the training pipeline? How would we remedy this?

for epoch in range(num_epochs):
    print(f"START EPOCH {epoch+1}")
    print("TRAINING")
    train(model, dl_train, optimizer, reporting_interval=80)
    print("TESTING")
    test(model, dl_test, reporting_interval=20)
    print("-"*30)

Generate#

prompts = [
    "We compared the prevalence of", # organ-specific autoantibodies in a group of Helicobacter..."
    "We compared the prevalence of",
    "We compared the prevalence of",
]

prompt_ids = dataset.tokenizer(prompts, return_tensors='pt')['input_ids']

# trim off unwanted [SEP] tokens which act like our special end-of-sequence token.
prompt_ids = prompt_ids[:,:-1]

# generate ids
gen_ids = generate(model.to('cpu'), prompt_ids, 50)
dataset.decode_batch(gen_ids)

prompts = [
    "The pytorch llm workshop was",
    "The pytorch llm workshop was",
    "The pytorch llm workshop was",
]

prompt_ids = dataset.tokenizer(prompts, return_tensors='pt')['input_ids']

# trim off unwanted [SEP] tokens which act like our special end-of-sequence token.
prompt_ids = prompt_ids[:,:-1]

# generate ids
gen_ids = generate(model, prompt_ids, 50)
dataset.decode_batch(gen_ids)