Introduction to Python III

In this notebook, we work through a typical data science exploratory analysis workflow:

1. Read in some data (using pandas)

2. Look at the raw data (pandas)

3. Compute some statistics (pandas)

4. Make some visualizations (matplotlib, seaborn, plotly)

Introduction to Pandas

So, what is Pandas?

Not this:

More like this:

But with code!

You may feel that removing the graphical interface from the spreadsheet is a step backwards. However, swapping buttons for code makes us much more efficient at complicated tasks (once we get used to it)

Loading the library

# pandas is usually aliased as "pd"
import pandas as pd

Reading in data

We will use the famous iris dataset.

# we can read in data from many formats. comma-separated values (csv) is a common one
# this csv is located at a url. It could just as easily be a file on your computer.
df = pd.read_csv("https://gist.githubusercontent.com/netj/8836201/raw/6f9306ad21398ea43cba4f7d537619d0e07d5ae3/iris.csv")

df

	sepal.length	sepal.width	petal.length	petal.width	variety
0	5.1	3.5	1.4	0.2	Setosa
1	4.9	3.0	1.4	0.2	Setosa
2	4.7	3.2	1.3	0.2	Setosa
3	4.6	3.1	1.5	0.2	Setosa
4	5.0	3.6	1.4	0.2	Setosa
...	...	...	...	...	...
145	6.7	3.0	5.2	2.3	Virginica
146	6.3	2.5	5.0	1.9	Virginica
147	6.5	3.0	5.2	2.0	Virginica
148	6.2	3.4	5.4	2.3	Virginica
149	5.9	3.0	5.1	1.8	Virginica

150 rows × 5 columns

When we read in the data, pandas creates a “dataframe” object. This is analogous to a spreadsheet in Excel.

type(df)

pandas.core.frame.DataFrame

No-one really knows the full extent of things you can do with a pandas dataframe (hyperbole).

You can browse the methods here: https://pandas.pydata.org/docs/reference/api/pandas.DataFrame.html

Basic attributes

First, let’s consider a few simple attributes:

# the columns:
df.columns

Index(['sepal.length', 'sepal.width', 'petal.length', 'petal.width',
       'variety'],
      dtype='object')

# the first few rows:
df.head()

	sepal.length	sepal.width	petal.length	petal.width	variety
0	5.1	3.5	1.4	0.2	Setosa
1	4.9	3.0	1.4	0.2	Setosa
2	4.7	3.2	1.3	0.2	Setosa
3	4.6	3.1	1.5	0.2	Setosa
4	5.0	3.6	1.4	0.2	Setosa

# the shape of the dataframe:
df.shape  # number of rows, number of columns

(150, 5)

# the data types of the columns:
df.dtypes

sepal.length    float64
sepal.width     float64
petal.length    float64
petal.width     float64
variety          object
dtype: object

Selecting data

# we can select a single column by name:
df['petal.width']
# an individial column is called a "series" in pandas

0      0.2
1      0.2
2      0.2
3      0.2
4      0.2
      ... 
145    2.3
146    1.9
147    2.0
148    2.3
149    1.8
Name: petal.width, Length: 150, dtype: float64

# we can select multiple columns by name:
df[['petal.width', 'petal.length']]

	petal.width	petal.length
0	0.2	1.4
1	0.2	1.4
2	0.2	1.3
3	0.2	1.5
4	0.2	1.4
...	...	...
145	2.3	5.2
146	1.9	5.0
147	2.0	5.2
148	2.3	5.4
149	1.8	5.1

150 rows × 2 columns

# we can select rows by index:
df.loc[0]

sepal.length       5.1
sepal.width        3.5
petal.length       1.4
petal.width        0.2
variety         Setosa
Name: 0, dtype: object

# we can select multiple rows by index:
df.loc[0:5]
# notice: the range is inclusive on both ends! why?

	sepal.length	sepal.width	petal.length	petal.width	variety
0	5.1	3.5	1.4	0.2	Setosa
1	4.9	3.0	1.4	0.2	Setosa
2	4.7	3.2	1.3	0.2	Setosa
3	4.6	3.1	1.5	0.2	Setosa
4	5.0	3.6	1.4	0.2	Setosa
5	5.4	3.9	1.7	0.4	Setosa

# we can select specific elements by row and column:
df.loc[0, 'petal.width']

0.2

# we can select a range of elements by row and column ranges: 
df.loc[0:5, 'petal.width':'variety']

	petal.width	variety
0	0.2	Setosa
1	0.2	Setosa
2	0.2	Setosa
3	0.2	Setosa
4	0.2	Setosa
5	0.4	Setosa

Basic math manipulations

# we can take the average of a column
df['petal.length'].mean()

# there are lots of other options we can perform, for example: min, max, median, mode, std, var, sum, count, etc.

3.7580000000000027

# what if we wanted to know the average of sepal.length and sepal.width for each sample?
df[['sepal.length', 'sepal.width']].mean(axis=1)

# here we use "axis=1" to specify that we are taking the average along the row rather than down the column.

0      4.30
1      3.95
2      3.95
3      3.85
4      4.30
       ... 
145    4.85
146    4.40
147    4.75
148    4.80
149    4.45
Length: 150, dtype: float64

# let's store this as a new column
df['sepal.mean'] = df[['sepal.length', 'sepal.width']].mean(axis=1)

df

	sepal.length	sepal.width	petal.length	petal.width	variety	sepal.mean
0	5.1	3.5	1.4	0.2	Setosa	4.30
1	4.9	3.0	1.4	0.2	Setosa	3.95
2	4.7	3.2	1.3	0.2	Setosa	3.95
3	4.6	3.1	1.5	0.2	Setosa	3.85
4	5.0	3.6	1.4	0.2	Setosa	4.30
...	...	...	...	...	...	...
145	6.7	3.0	5.2	2.3	Virginica	4.85
146	6.3	2.5	5.0	1.9	Virginica	4.40
147	6.5	3.0	5.2	2.0	Virginica	4.75
148	6.2	3.4	5.4	2.3	Virginica	4.80
149	5.9	3.0	5.1	1.8	Virginica	4.45

150 rows × 6 columns

# we could also have computed the mean by directly manipulating the columns:
df['sepal.mean.2'] = (df['sepal.length'] + df['sepal.width']) / 2

df

	sepal.length	sepal.width	petal.length	petal.width	variety	sepal.mean	sepal.mean.2
0	5.1	3.5	1.4	0.2	Setosa	4.30	4.30
1	4.9	3.0	1.4	0.2	Setosa	3.95	3.95
2	4.7	3.2	1.3	0.2	Setosa	3.95	3.95
3	4.6	3.1	1.5	0.2	Setosa	3.85	3.85
4	5.0	3.6	1.4	0.2	Setosa	4.30	4.30
...	...	...	...	...	...	...	...
145	6.7	3.0	5.2	2.3	Virginica	4.85	4.85
146	6.3	2.5	5.0	1.9	Virginica	4.40	4.40
147	6.5	3.0	5.2	2.0	Virginica	4.75	4.75
148	6.2	3.4	5.4	2.3	Virginica	4.80	4.80
149	5.9	3.0	5.1	1.8	Virginica	4.45	4.45

150 rows × 7 columns

Save to a file

# we can write the modified dataframne to a new csv file
df.to_csv('iris_with_means.csv')

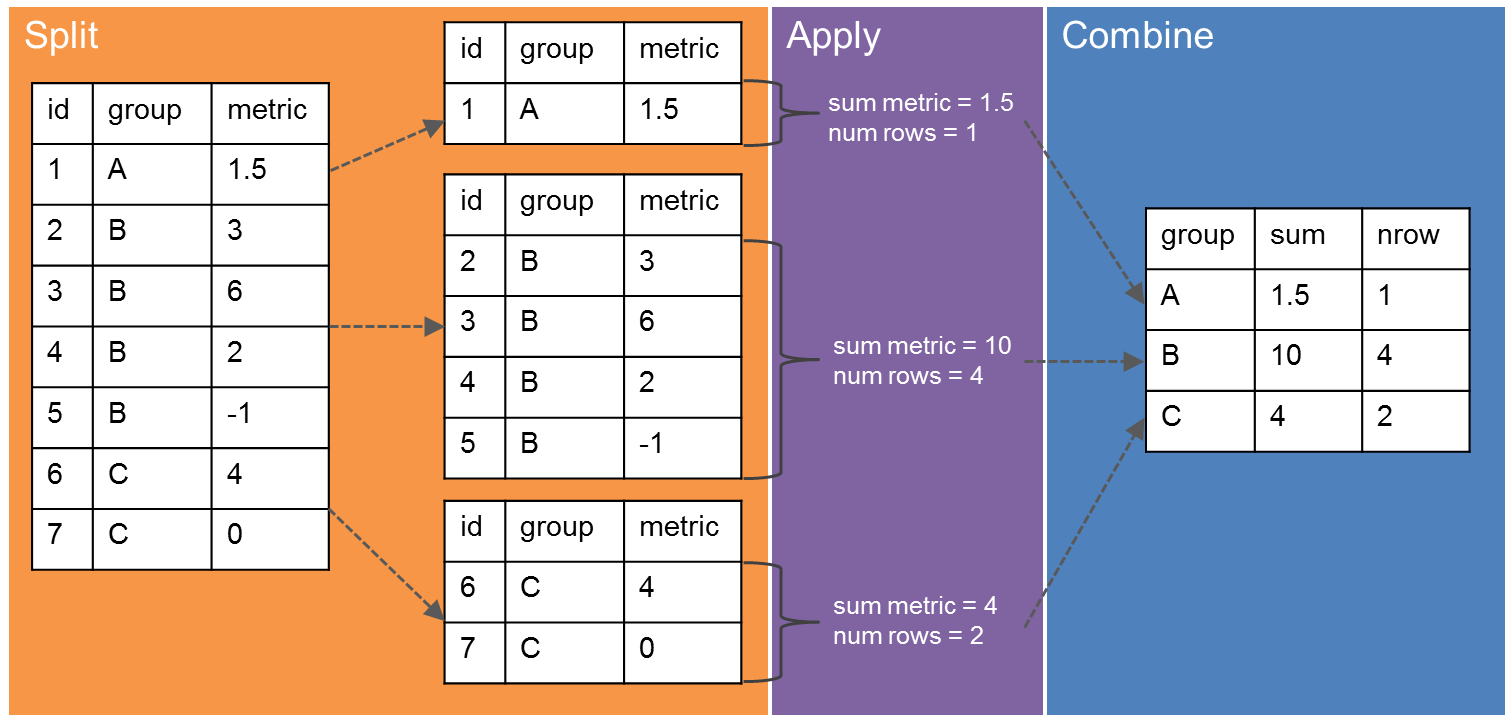
Powerful data manipulation with “Split, Apply, Combine”

“Split, Apply, Combine” refers to the common practice of splitting up a dataset into relevant chunks, doing some computation on those chunks, then combining the output into a single table. In pandas, we can break up the data into groups using the groupby method. We can then apply our computation on the grouped data. If we set things up right, pandas will combine the results automatically. Image credit.

# load the original iris dataset file
df = pd.read_csv("https://gist.githubusercontent.com/netj/8836201/raw/6f9306ad21398ea43cba4f7d537619d0e07d5ae3/iris.csv")
df

	sepal.length	sepal.width	petal.length	petal.width	variety
0	5.1	3.5	1.4	0.2	Setosa
1	4.9	3.0	1.4	0.2	Setosa
2	4.7	3.2	1.3	0.2	Setosa
3	4.6	3.1	1.5	0.2	Setosa
4	5.0	3.6	1.4	0.2	Setosa
...	...	...	...	...	...
145	6.7	3.0	5.2	2.3	Virginica
146	6.3	2.5	5.0	1.9	Virginica
147	6.5	3.0	5.2	2.0	Virginica
148	6.2	3.4	5.4	2.3	Virginica
149	5.9	3.0	5.1	1.8	Virginica

150 rows × 5 columns

groupby

Group by allows us to split up the data.

# what do we get just call groupby? 
df.groupby('variety')
# answer: a special DataFrameGroupBy object

<pandas.core.groupby.generic.DataFrameGroupBy object at 0x149145353b80>

# we can iterate over this data structure manually: 
for g, d in df.groupby('variety'): 
    print(g)
    display(d.head(2))

Setosa

	sepal.length	sepal.width	petal.length	petal.width	variety
0	5.1	3.5	1.4	0.2	Setosa
1	4.9	3.0	1.4	0.2	Setosa

Versicolor

	sepal.length	sepal.width	petal.length	petal.width	variety
50	7.0	3.2	4.7	1.4	Versicolor
51	6.4	3.2	4.5	1.5	Versicolor

Virginica

	sepal.length	sepal.width	petal.length	petal.width	variety
100	6.3	3.3	6.0	2.5	Virginica
101	5.8	2.7	5.1	1.9	Virginica

# we can even perform split-apply-combine manually
# for instance, we can compute the average 'sepal.length' for each set

variety = []
sepal_length = []

# 1. Split
for g, d in df.groupby('variety'): 
    variety.append(g)
    # 2. Apply:
    sepal_length.append(d['sepal.length'].mean())
    
# 3. Combine
pd.DataFrame({'variety': variety, 'sepal.length': sepal_length})

	variety	sepal.length
0	Setosa	5.006
1	Versicolor	5.936
2	Virginica	6.588

# but this is such a common workflow that pandas makes it easy
df.groupby('variety', as_index=False)['sepal.length'].mean()

	variety	sepal.length
0	Setosa	5.006
1	Versicolor	5.936
2	Virginica	6.588

# and, using the pandas way, we can compute the mean of all variables without writing more code
df.groupby('variety', as_index=False).mean()

	variety	sepal.length	sepal.width	petal.length	petal.width
0	Setosa	5.006	3.428	1.462	0.246
1	Versicolor	5.936	2.770	4.260	1.326
2	Virginica	6.588	2.974	5.552	2.026

# we can even compute multiple metrics per column using the `agg` method:
df.groupby('variety', as_index=False).agg(['mean', 'std', 'sem', 'count'])
# advanced note: because we have multiple functions for each variable, pandas has created a multi-index for the columns

	sepal.length				sepal.width				petal.length				petal.width
	mean	std	sem	count	mean	std	sem	count	mean	std	sem	count	mean	std	sem	count
variety
Setosa	5.006	0.352490	0.049850	50	3.428	0.379064	0.053608	50	1.462	0.173664	0.024560	50	0.246	0.105386	0.014904	50
Versicolor	5.936	0.516171	0.072998	50	2.770	0.313798	0.044378	50	4.260	0.469911	0.066455	50	1.326	0.197753	0.027966	50
Virginica	6.588	0.635880	0.089927	50	2.974	0.322497	0.045608	50	5.552	0.551895	0.078050	50	2.026	0.274650	0.038841	50

# pretty colors if you want
df.groupby('variety').agg(['mean', 'std', 'sem', 'count']).style.background_gradient('Blues')

	sepal.length				sepal.width				petal.length				petal.width
	mean	std	sem	count	mean	std	sem	count	mean	std	sem	count	mean	std	sem	count
variety
Setosa	5.006000	0.352490	0.049850	50	3.428000	0.379064	0.053608	50	1.462000	0.173664	0.024560	50	0.246000	0.105386	0.014904	50
Versicolor	5.936000	0.516171	0.072998	50	2.770000	0.313798	0.044378	50	4.260000	0.469911	0.066455	50	1.326000	0.197753	0.027966	50
Virginica	6.588000	0.635880	0.089927	50	2.974000	0.322497	0.045608	50	5.552000	0.551895	0.078050	50	2.026000	0.274650	0.038841	50

apply

The above methods worked because pandas implements special “mean”, “std”, “sem”, and “count” for the grouped data frame object. But what if we want to apply some custom function to the grouped data?

For example, say we wanted to apply standard-normal scaling to the sepal.length variable within each variety group? If \(x\) is sepal.length, we want to compute a new variable $\( x' = \frac{x - \mu_x}{\sigma_x} \)\( where \)\mu_x\( and \)\sigma_x$ are computed separately within each variety.

How do we do this in pandas? This is where the apply method comes in. See the documentation for more tricks.

# first define a function that applies to a specific element
def standard_scaler(data):
    """Standardize the data"""
    return (data - data.mean()) / data.std()

# then use apply to loop the function over the column
df_scaled = df.set_index('variety').groupby('variety', group_keys=False).apply(standard_scaler)
df_scaled

	sepal.length	sepal.width	petal.length	petal.width
variety
Setosa	0.266674	0.189941	-0.357011	-0.436492
Setosa	-0.300718	-1.129096	-0.357011	-0.436492
Setosa	-0.868111	-0.601481	-0.932836	-0.436492
Setosa	-1.151807	-0.865288	0.218813	-0.436492
Setosa	-0.017022	0.453749	-0.357011	-0.436492
...	...	...	...	...
Virginica	0.176134	0.080621	-0.637803	0.997633
Virginica	-0.452916	-1.469783	-1.000191	-0.458766
Virginica	-0.138391	0.080621	-0.637803	-0.094666
Virginica	-0.610178	1.320944	-0.275415	0.997633
Virginica	-1.081966	0.080621	-0.818997	-0.822865

150 rows × 4 columns

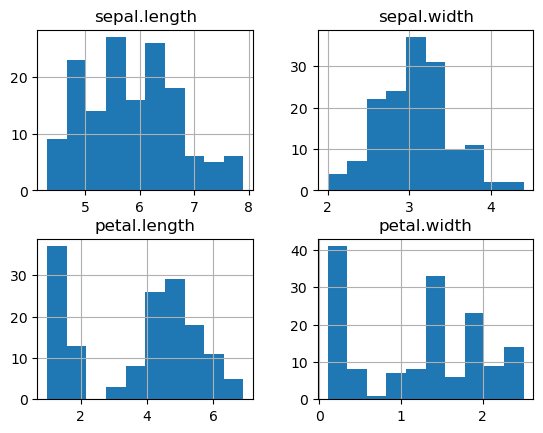
print("Original variables:")
_ = df.set_index('variety').hist()

Original variables:

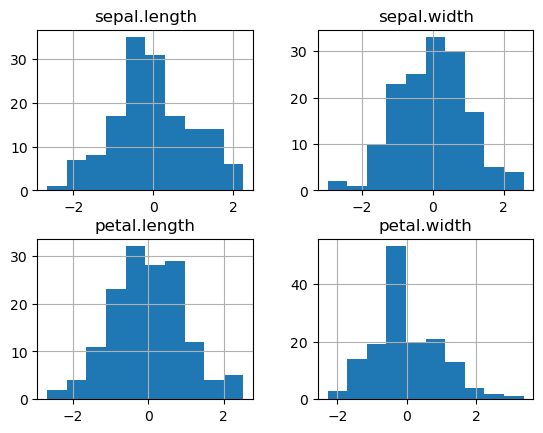
print("Scaled variables:")
_ = df_scaled.hist()

Scaled variables:

melt and pivot_table

Often our data contains multiple measurements, with each measurement using one column. Sometimes, it is more convenient to place all of the measurements in a single column, with an additional column to indicate which measurement the value represents.

Take for example the iris dataset.

Original:

df.head()

	sepal.length	sepal.width	petal.length	petal.width	variety
0	5.1	3.5	1.4	0.2	Setosa
1	4.9	3.0	1.4	0.2	Setosa
2	4.7	3.2	1.3	0.2	Setosa
3	4.6	3.1	1.5	0.2	Setosa
4	5.0	3.6	1.4	0.2	Setosa

Melted version:

df.melt(id_vars = ['variety'])

	variety	variable	value
0	Setosa	sepal.length	5.1
1	Setosa	sepal.length	4.9
2	Setosa	sepal.length	4.7
3	Setosa	sepal.length	4.6
4	Setosa	sepal.length	5.0
...	...	...	...
595	Virginica	petal.width	2.3
596	Virginica	petal.width	1.9
597	Virginica	petal.width	2.0
598	Virginica	petal.width	2.3
599	Virginica	petal.width	1.8

600 rows × 3 columns

Notice that this results in a narrower and longer dataframe. By default, pandas assigns the names variable and value to the column giving the measurement name and the column holding the measurement itself, respectively. We can change these by passing in the right arguments:

df.melt(id_vars = ['variety'], var_name='measurement_name', value_name='measurement_value')

	variety	measurement_name	measurement_value
0	Setosa	sepal.length	5.1
1	Setosa	sepal.length	4.9
2	Setosa	sepal.length	4.7
3	Setosa	sepal.length	4.6
4	Setosa	sepal.length	5.0
...	...	...	...
595	Virginica	petal.width	2.3
596	Virginica	petal.width	1.9
597	Virginica	petal.width	2.0
598	Virginica	petal.width	2.3
599	Virginica	petal.width	1.8

600 rows × 3 columns

---

Question: Why would we want to melt a dataframe?

---

df_melted = df.melt(id_vars = ['variety'])

df_melted.head()

	variety	variable	value
0	Setosa	sepal.length	5.1
1	Setosa	sepal.length	4.9
2	Setosa	sepal.length	4.7
3	Setosa	sepal.length	4.6
4	Setosa	sepal.length	5.0

df_melted.groupby(['variety', 'variable']).agg(['mean', 'sem'])

		value
		mean	sem
variety	variable
Setosa	petal.length	1.462	0.024560
	petal.width	0.246	0.014904
	sepal.length	5.006	0.049850
	sepal.width	3.428	0.053608
Versicolor	petal.length	4.260	0.066455
	petal.width	1.326	0.027966
	sepal.length	5.936	0.072998
	sepal.width	2.770	0.044378
Virginica	petal.length	5.552	0.078050
	petal.width	2.026	0.038841
	sepal.length	6.588	0.089927
	sepal.width	2.974	0.045608

Compare this with the same operation on the original data

df.groupby(['variety']).agg(['mean', 'sem'])

	sepal.length		sepal.width		petal.length		petal.width
	mean	sem	mean	sem	mean	sem	mean	sem
variety
Setosa	5.006	0.049850	3.428	0.053608	1.462	0.024560	0.246	0.014904
Versicolor	5.936	0.072998	2.770	0.044378	4.260	0.066455	1.326	0.027966
Virginica	6.588	0.089927	2.974	0.045608	5.552	0.078050	2.026	0.038841

# with the melted data, we can easily plot the distribution of each variable for each variety
import matplotlib.pyplot as plt

for key, group in df_melted.groupby(['variety', 'variable']):
    plt.hist(group['value'], label=" ".join(key))
_ = plt.legend()

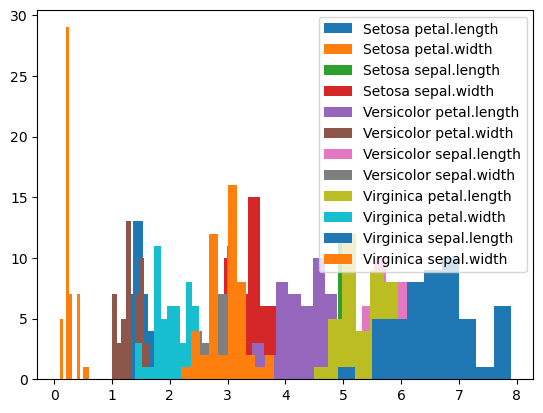
Compare with how we have to produce this plot from the original dataframe:

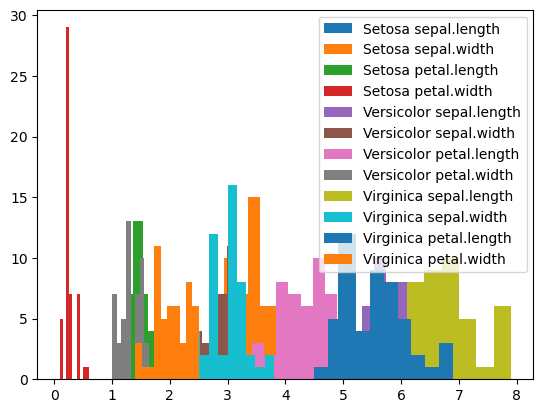
# with the original dataframe, we need a second for loop over the different columns we want to plot
for key, group in df.groupby('variety'):
    for col in ["sepal.length", "sepal.width", "petal.length", "petal.width"]:
        plt.hist(group[col], label=f"{key} {col}")
_ = plt.legend()

pivot_table is the conceptually the opposite of melt. It allows us to convert a column with variable names into multiple columns.

Let’s use pivot table on our melted dataframe. To do so, we need to specify the following:

• index: which columns will be used to uniquely specify the rows in the resulting dataframe. In this case, we want variety.

• columns: which columns will be converted into new columns in the resulting dataframe. In this case, we want variable.

• values: which column contains the values that will be used to populate the new dataframe. In this case, we want value.

df_melted.pivot_table(index = 'variety', columns='variable', values='value')

variable	petal.length	petal.width	sepal.length	sepal.width
variety
Setosa	1.462	0.246	5.006	3.428
Versicolor	4.260	1.326	5.936	2.770
Virginica	5.552	2.026	6.588	2.974

Notice that we only have 3 rows! This is because the provided index (variety) does not uniquely specify the original rows in our dataframe. When pivoting, pandas applied the default aggregation function – mean – to fill the cells.

We can change the aggregation function as needed:

df_melted.pivot_table(index = 'variety', columns='variable', values='value', aggfunc='max')

variable	petal.length	petal.width	sepal.length	sepal.width
variety
Setosa	1.9	0.6	5.8	4.4
Versicolor	5.1	1.8	7.0	3.4
Virginica	6.9	2.5	7.9	3.8

# here we provide a custom lambda aggfunc. This shows how pivot_table
# can be used to make nice human-readable tables
df_melted.pivot_table(index = 'variety', columns='variable', values='value', aggfunc=lambda x: f"{x.mean():0.2f}+/-{1.96*x.sem():0.2f}")

variable	petal.length	petal.width	sepal.length	sepal.width
variety
Setosa	1.46+/-0.05	0.25+/-0.03	5.01+/-0.10	3.43+/-0.11
Versicolor	4.26+/-0.13	1.33+/-0.05	5.94+/-0.14	2.77+/-0.09
Virginica	5.55+/-0.15	2.03+/-0.08	6.59+/-0.18	2.97+/-0.09

Understanding your data with distribution plots

The “taxis” dataset

# seaborn is a popular plotting library that works well with pandas
import seaborn as sns

df = sns.load_dataset('taxis')
df

	pickup	dropoff	passengers	distance	fare	tip	tolls	total	color	payment	pickup_zone	dropoff_zone	pickup_borough	dropoff_borough
0	2019-03-23 20:21:09	2019-03-23 20:27:24	1	1.60	7.0	2.15	0.0	12.95	yellow	credit card	Lenox Hill West	UN/Turtle Bay South	Manhattan	Manhattan
1	2019-03-04 16:11:55	2019-03-04 16:19:00	1	0.79	5.0	0.00	0.0	9.30	yellow	cash	Upper West Side South	Upper West Side South	Manhattan	Manhattan
2	2019-03-27 17:53:01	2019-03-27 18:00:25	1	1.37	7.5	2.36	0.0	14.16	yellow	credit card	Alphabet City	West Village	Manhattan	Manhattan
3	2019-03-10 01:23:59	2019-03-10 01:49:51	1	7.70	27.0	6.15	0.0	36.95	yellow	credit card	Hudson Sq	Yorkville West	Manhattan	Manhattan
4	2019-03-30 13:27:42	2019-03-30 13:37:14	3	2.16	9.0	1.10	0.0	13.40	yellow	credit card	Midtown East	Yorkville West	Manhattan	Manhattan
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
6428	2019-03-31 09:51:53	2019-03-31 09:55:27	1	0.75	4.5	1.06	0.0	6.36	green	credit card	East Harlem North	Central Harlem North	Manhattan	Manhattan
6429	2019-03-31 17:38:00	2019-03-31 18:34:23	1	18.74	58.0	0.00	0.0	58.80	green	credit card	Jamaica	East Concourse/Concourse Village	Queens	Bronx
6430	2019-03-23 22:55:18	2019-03-23 23:14:25	1	4.14	16.0	0.00	0.0	17.30	green	cash	Crown Heights North	Bushwick North	Brooklyn	Brooklyn
6431	2019-03-04 10:09:25	2019-03-04 10:14:29	1	1.12	6.0	0.00	0.0	6.80	green	credit card	East New York	East Flatbush/Remsen Village	Brooklyn	Brooklyn
6432	2019-03-13 19:31:22	2019-03-13 19:48:02	1	3.85	15.0	3.36	0.0	20.16	green	credit card	Boerum Hill	Windsor Terrace	Brooklyn	Brooklyn

6433 rows × 14 columns

Questions we might want to answer based on this data:

• How does the fare depend on other factors like travel distance, number of passengers, time of day, and pickup zone?

• What are the most common pickup and dropoff locations in the data?

• What factors influence the travel time?

• Do green cabs charge bigger fares than yellow cabs?

• Can you think of any other questions?

Distribution plots / density plots can help us start to answer these questions.

Histogram for 1D data

_ = plt.hist(df.fare)

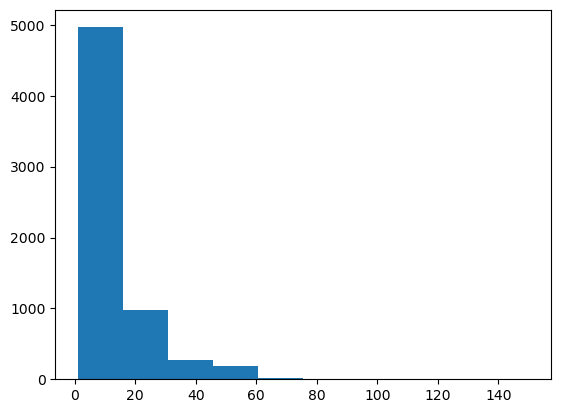
Problems:

• No labels

• Not enough bins

Let’s improve this histogram

plt.hist(df.fare, bins=100)
plt.xlabel('Fare')
plt.ylabel('Count')

Text(0, 0.5, 'Count')

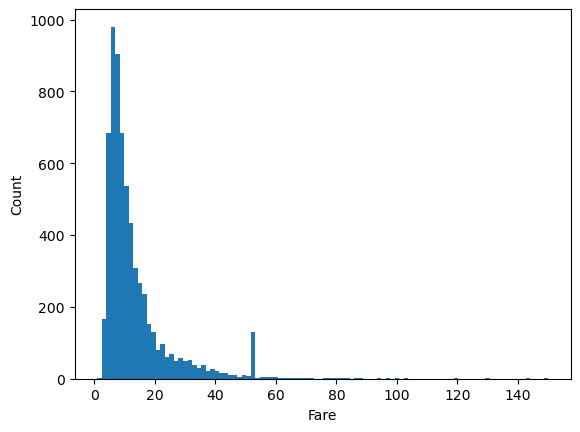
That’s much better, but there’s a lot of wasted space due to some very high Fare values. Let’s manually set the limit to get rid of this.

plt.hist(df.fare, bins=100)
plt.xlabel('Fare')
plt.ylabel('Count')
plt.xlim(0,80)

(0.0, 80.0)

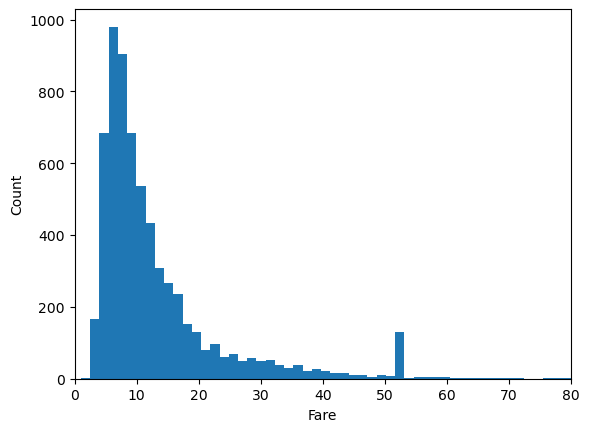
Given the nature of the distribution, we may wish to put the x-axis on a log scale.

# we need the numpy library to take the log of the fare
import numpy as np

# we can do this by taking the log of the fare, in which case the bins are uniform in log space...
plt.hist(np.log10(df.fare), bins=100)
plt.xlabel(r'$\log_{10}(\mathrm{Fare})$')
plt.ylabel('Count')
plt.grid()

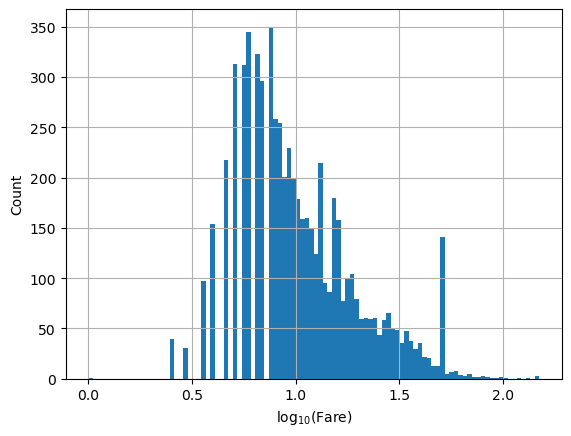
# or by converting the axis to log-scale after the fact. In this case, bins are non-uniform
# in log space.
plt.hist(df.fare, bins=100)
plt.xlabel('Fare')
plt.ylabel('Count')
plt.xlim(1,80)
plt.semilogx()
plt.grid()

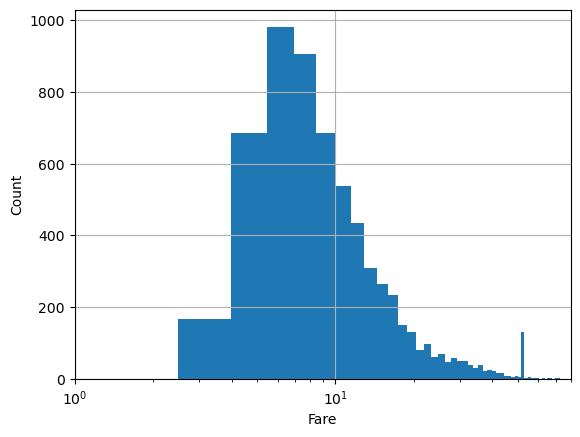
By default, hist gives number of samples for the y axis. Sometimes, we want the percentage of samples in the bin instead.

plt.hist(df.fare, bins=100, density=True)
plt.xlabel('Fare')
plt.ylabel('Density')
plt.xlim(1,80)
plt.semilogx()
plt.grid()

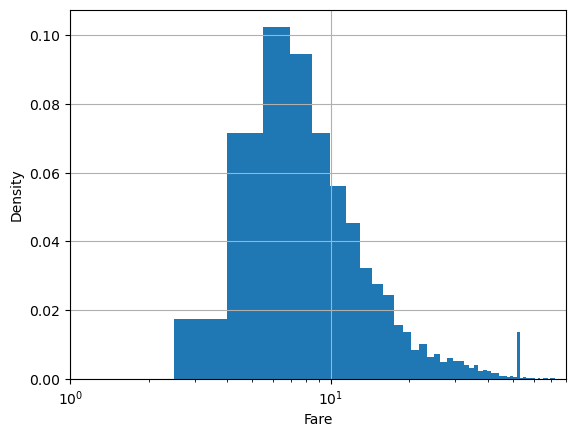
Sometimes we want the log-density instead:

plt.hist(df.fare, bins=100, density=True, log=True)
plt.xlabel('Fare')
plt.ylabel('Density')
plt.xlim(1,80)
plt.grid()

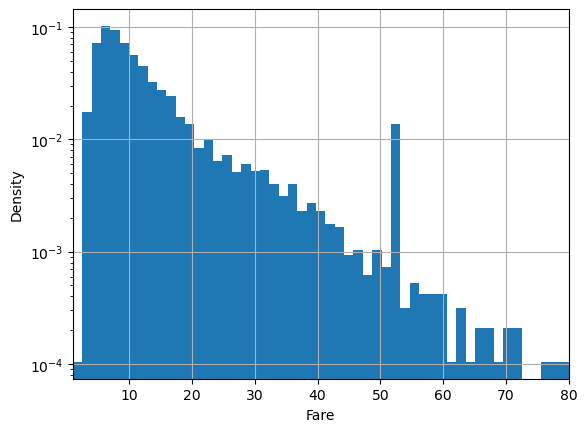
Kernel Density Estimation

Sometimes we want smooth approximations to our data distribution. Smooth approximations can show us the underlying pattern while removing noise due to small sample size. Kernel Density Estimation is just a fancy name for a method of fitting smooth approximations to data distributions. The seaborn library, which we loaded with alias sns provides convenient methods for fitting and plotting kernel density estimates.

sns.kdeplot(data=df, x='fare')

<AxesSubplot:xlabel='fare', ylabel='Density'>

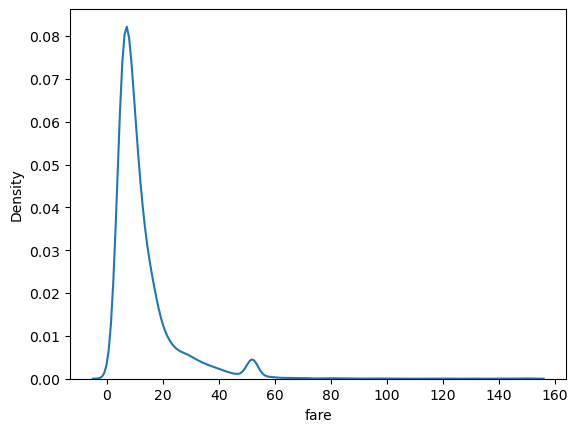
Seaborn functions like kdeplot have about a jillion arguments

sns.kdeplot?

Signature:
sns.kdeplot(
    x=None,
    *,
    y=None,
    shade=None,
    vertical=False,
    kernel=None,
    bw=None,
    gridsize=200,
    cut=3,
    clip=None,
    legend=True,
    cumulative=False,
    shade_lowest=None,
    cbar=False,
    cbar_ax=None,
    cbar_kws=None,
    ax=None,
    weights=None,
    hue=None,
    palette=None,
    hue_order=None,
    hue_norm=None,
    multiple='layer',
    common_norm=True,
    common_grid=False,
    levels=10,
    thresh=0.05,
    bw_method='scott',
    bw_adjust=1,
    log_scale=None,
    color=None,
    fill=None,
    data=None,
    data2=None,
    warn_singular=True,
    **kwargs,
)
Docstring:
Plot univariate or bivariate distributions using kernel density estimation.

A kernel density estimate (KDE) plot is a method for visualizing the
distribution of observations in a dataset, analagous to a histogram. KDE
represents the data using a continuous probability density curve in one or
more dimensions.

The approach is explained further in the :ref:`user guide <tutorial_kde>`.

Relative to a histogram, KDE can produce a plot that is less cluttered and
more interpretable, especially when drawing multiple distributions. But it
has the potential to introduce distortions if the underlying distribution is
bounded or not smooth. Like a histogram, the quality of the representation
also depends on the selection of good smoothing parameters.

Parameters
----------
x, y : vectors or keys in ``data``
    Variables that specify positions on the x and y axes.
shade : bool
    Alias for ``fill``. Using ``fill`` is recommended.
vertical : bool
    Orientation parameter.

    .. deprecated:: 0.11.0
       specify orientation by assigning the ``x`` or ``y`` variables.

kernel : str
    Function that defines the kernel.

    .. deprecated:: 0.11.0
       support for non-Gaussian kernels has been removed.

bw : str, number, or callable
    Smoothing parameter.

    .. deprecated:: 0.11.0
       see ``bw_method`` and ``bw_adjust``.

gridsize : int
    Number of points on each dimension of the evaluation grid.
cut : number, optional
    Factor, multiplied by the smoothing bandwidth, that determines how
    far the evaluation grid extends past the extreme datapoints. When
    set to 0, truncate the curve at the data limits.
clip : pair of numbers or None, or a pair of such pairs
    Do not evaluate the density outside of these limits.
legend : bool
    If False, suppress the legend for semantic variables.
cumulative : bool, optional
    If True, estimate a cumulative distribution function.
shade_lowest : bool
    If False, the area below the lowest contour will be transparent

    .. deprecated:: 0.11.0
       see ``thresh``.

cbar : bool
    If True, add a colorbar to annotate the color mapping in a bivariate plot.
    Note: Does not currently support plots with a ``hue`` variable well.
cbar_ax : :class:`matplotlib.axes.Axes`
    Pre-existing axes for the colorbar.
cbar_kws : dict
    Additional parameters passed to :meth:`matplotlib.figure.Figure.colorbar`.
ax : :class:`matplotlib.axes.Axes`
    Pre-existing axes for the plot. Otherwise, call :func:`matplotlib.pyplot.gca`
    internally.
weights : vector or key in ``data``
    If provided, weight the kernel density estimation using these values.
hue : vector or key in ``data``
    Semantic variable that is mapped to determine the color of plot elements.
palette : string, list, dict, or :class:`matplotlib.colors.Colormap`
    Method for choosing the colors to use when mapping the ``hue`` semantic.
    String values are passed to :func:`color_palette`. List or dict values
    imply categorical mapping, while a colormap object implies numeric mapping.
hue_order : vector of strings
    Specify the order of processing and plotting for categorical levels of the
    ``hue`` semantic.
hue_norm : tuple or :class:`matplotlib.colors.Normalize`
    Either a pair of values that set the normalization range in data units
    or an object that will map from data units into a [0, 1] interval. Usage
    implies numeric mapping.
multiple : {{"layer", "stack", "fill"}}
    Method for drawing multiple elements when semantic mapping creates subsets.
    Only relevant with univariate data.
common_norm : bool
    If True, scale each conditional density by the number of observations
    such that the total area under all densities sums to 1. Otherwise,
    normalize each density independently.
common_grid : bool
    If True, use the same evaluation grid for each kernel density estimate.
    Only relevant with univariate data.
levels : int or vector
    Number of contour levels or values to draw contours at. A vector argument
    must have increasing values in [0, 1]. Levels correspond to iso-proportions
    of the density: e.g., 20% of the probability mass will lie below the
    contour drawn for 0.2. Only relevant with bivariate data.
thresh : number in [0, 1]
    Lowest iso-proportion level at which to draw a contour line. Ignored when
    ``levels`` is a vector. Only relevant with bivariate data.
bw_method : string, scalar, or callable, optional
    Method for determining the smoothing bandwidth to use; passed to
    :class:`scipy.stats.gaussian_kde`.
bw_adjust : number, optional
    Factor that multiplicatively scales the value chosen using
    ``bw_method``. Increasing will make the curve smoother. See Notes.
log_scale : bool or number, or pair of bools or numbers
    Set axis scale(s) to log. A single value sets the data axis for univariate
    distributions and both axes for bivariate distributions. A pair of values
    sets each axis independently. Numeric values are interpreted as the desired
    base (default 10). If `False`, defer to the existing Axes scale.
color : :mod:`matplotlib color <matplotlib.colors>`
    Single color specification for when hue mapping is not used. Otherwise, the
    plot will try to hook into the matplotlib property cycle.
fill : bool or None
    If True, fill in the area under univariate density curves or between
    bivariate contours. If None, the default depends on ``multiple``.
data : :class:`pandas.DataFrame`, :class:`numpy.ndarray`, mapping, or sequence
    Input data structure. Either a long-form collection of vectors that can be
    assigned to named variables or a wide-form dataset that will be internally
    reshaped.
warn_singular : bool
    If True, issue a warning when trying to estimate the density of data
    with zero variance.
kwargs
    Other keyword arguments are passed to one of the following matplotlib
    functions:

    - :meth:`matplotlib.axes.Axes.plot` (univariate, ``fill=False``),
    - :meth:`matplotlib.axes.Axes.fill_between` (univariate, ``fill=True``),
    - :meth:`matplotlib.axes.Axes.contour` (bivariate, ``fill=False``),
    - :meth:`matplotlib.axes.contourf` (bivariate, ``fill=True``).

Returns
-------
:class:`matplotlib.axes.Axes`
    The matplotlib axes containing the plot.

See Also
--------
displot : Figure-level interface to distribution plot functions.
histplot : Plot a histogram of binned counts with optional normalization or smoothing.
ecdfplot : Plot empirical cumulative distribution functions.
jointplot : Draw a bivariate plot with univariate marginal distributions.
violinplot : Draw an enhanced boxplot using kernel density estimation.

Notes
-----

The *bandwidth*, or standard deviation of the smoothing kernel, is an
important parameter. Misspecification of the bandwidth can produce a
distorted representation of the data. Much like the choice of bin width in a
histogram, an over-smoothed curve can erase true features of a
distribution, while an under-smoothed curve can create false features out of
random variability. The rule-of-thumb that sets the default bandwidth works
best when the true distribution is smooth, unimodal, and roughly bell-shaped.
It is always a good idea to check the default behavior by using ``bw_adjust``
to increase or decrease the amount of smoothing.

Because the smoothing algorithm uses a Gaussian kernel, the estimated density
curve can extend to values that do not make sense for a particular dataset.
For example, the curve may be drawn over negative values when smoothing data
that are naturally positive. The ``cut`` and ``clip`` parameters can be used
to control the extent of the curve, but datasets that have many observations
close to a natural boundary may be better served by a different visualization
method.

Similar considerations apply when a dataset is naturally discrete or "spiky"
(containing many repeated observations of the same value). Kernel density
estimation will always produce a smooth curve, which would be misleading
in these situations.

The units on the density axis are a common source of confusion. While kernel
density estimation produces a probability distribution, the height of the curve
at each point gives a density, not a probability. A probability can be obtained
only by integrating the density across a range. The curve is normalized so
that the integral over all possible values is 1, meaning that the scale of
the density axis depends on the data values.

Examples
--------

.. include:: ../docstrings/kdeplot.rst
File:      /software/spackages/linux-rocky8-x86_64/gcc-9.5.0/anaconda3-2022.10-dtqfczcbv33ugxmsznhll4vjexdcxjfn/lib/python3.9/site-packages/seaborn/distributions.py
Type:      function

But seaborn uses matplotlib under the hood. So we can use some matplotlib commands to customize the look.

sns.kdeplot(data=df, x='fare')
plt.xlabel('Fare')
plt.xlim(1,80)
plt.semilogx()
plt.grid()

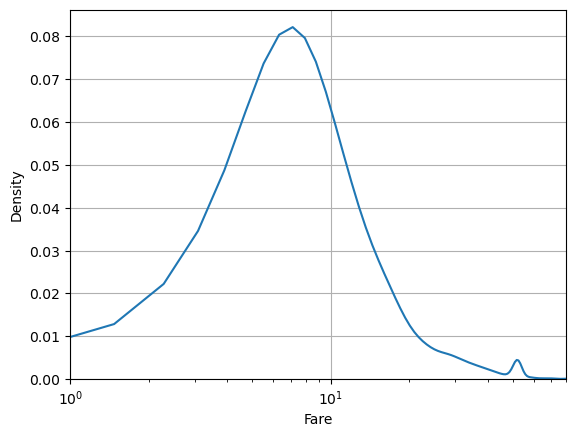
In KDE, it’s important to correctly set the smoothness parameter called bw_method for bin width method. Too large and you remove important structure in your data. Too small and you are fitting the noise.

sns.kdeplot(data=df, x='fare', bw_method=0.01, label='Too small')
sns.kdeplot(data=df, x='fare', bw_method=1, label='Too large')
sns.kdeplot(data=df, x='fare', bw_method=0.1, label='Juuuust right')
plt.xlabel('Fare')
plt.xlim(1,40)
plt.grid()
plt.legend()

<matplotlib.legend.Legend at 0x14912d33b280>

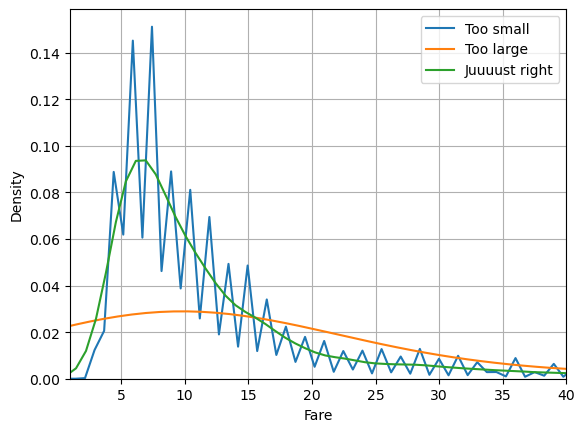
It can be useful to compare with a histogram to make sure you’re getting it right:

plt.hist(df.fare, bins=100, label='histogram', density=True, alpha=0.5)
sns.kdeplot(data=df, x='fare', bw_method=0.1, label='Juuuust right')
plt.xlabel('Fare')
plt.xlim(1,40)
plt.grid()
plt.legend()

<matplotlib.legend.Legend at 0x14913a1cba60>

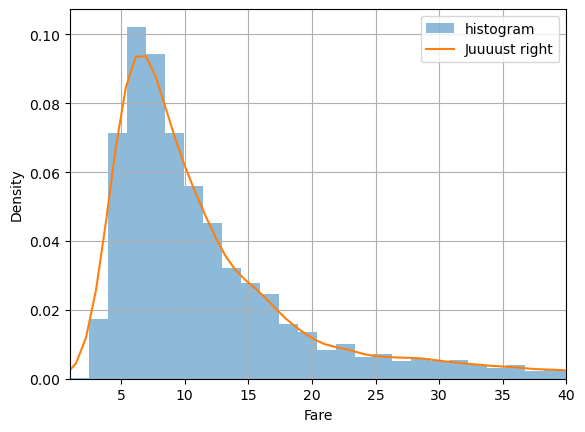
Seaborn makes it easy to group our data:

df.passengers = df.passengers.astype(str)
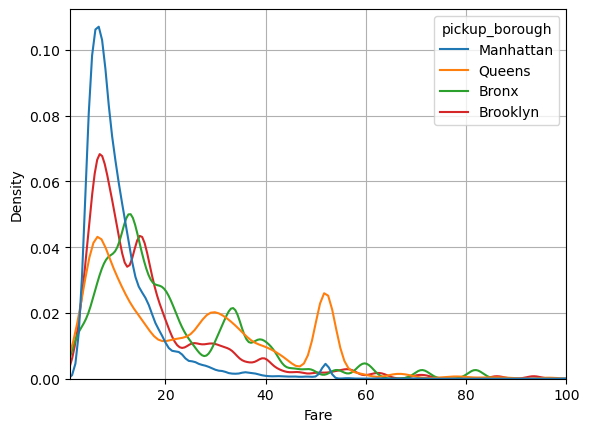
sns.kdeplot(data=df, x='fare', hue='pickup_borough', bw_method=0.1, common_norm=False)
plt.xlabel('Fare')
plt.xlim(1,100)
plt.grid()

Kernel Density Estimation in 2D

Kernel Density Estimation is especially useful in 2D.

Let’s return to the iris dataset and take, for instance, the distribution of petal_length and sepal_length

df = sns.load_dataset('iris')

sns.scatterplot(data=df, x='sepal_width', y='sepal_length')

<AxesSubplot:xlabel='sepal_width', ylabel='sepal_length'>

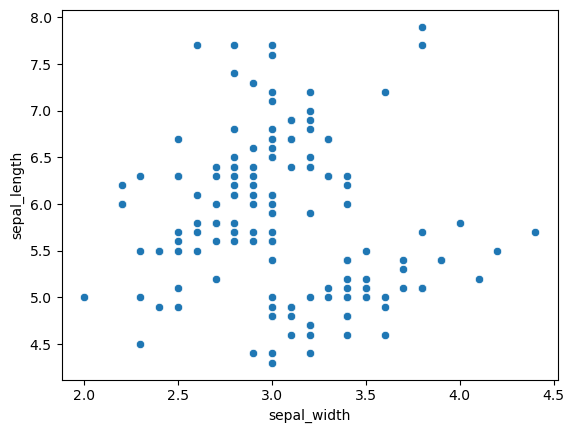
It looks like there are two groupings in the data. We can use KDE in two dimensions to visualize the distribution more clearly.

sns.displot(df, x='sepal_width', y='sepal_length', kind='kde')

<seaborn.axisgrid.FacetGrid at 0x149139f2b040>

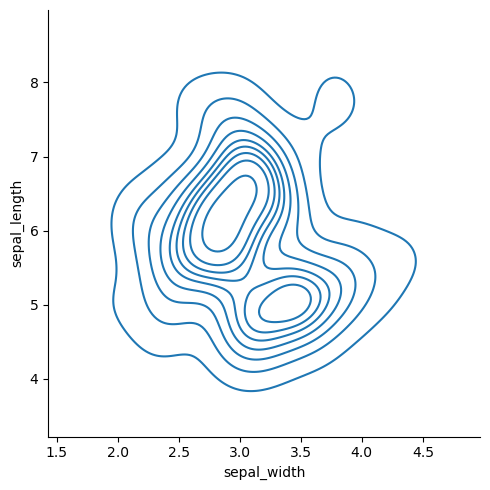
The data looks bi-modal. That is, there are two peaks. What could explain these two peaks?

sns.displot(df, x='sepal_width', y='sepal_length', hue='species', kind='kde')

<seaborn.axisgrid.FacetGrid at 0x149139cf4970>

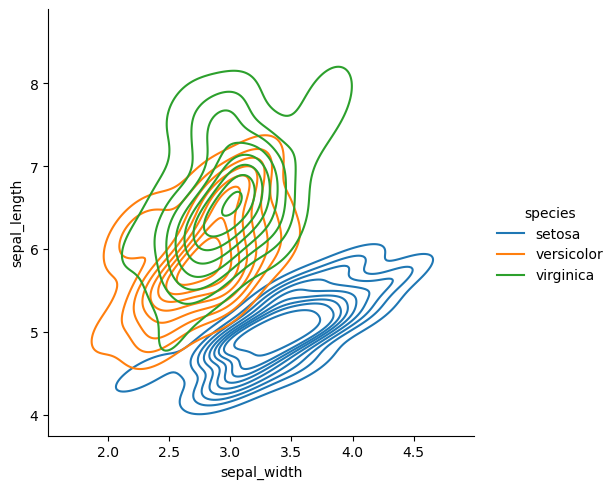
Now we can clearly see where the two peaks are coming from.

There are many ways to style the kde plots.

sns.displot(data=df, x='sepal_width', y='sepal_length', hue='species', fill=True, kind='kde')

<seaborn.axisgrid.FacetGrid at 0x14913a1cbd60>

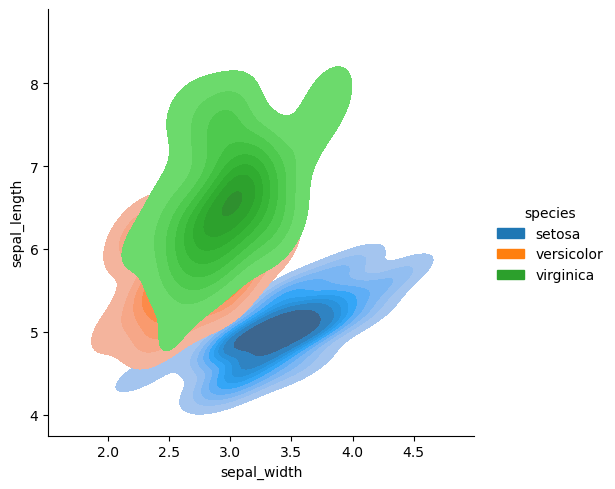
sns.displot(data=df, x='sepal_width', y='sepal_length', hue='species')

<seaborn.axisgrid.FacetGrid at 0x14913a0d5070>

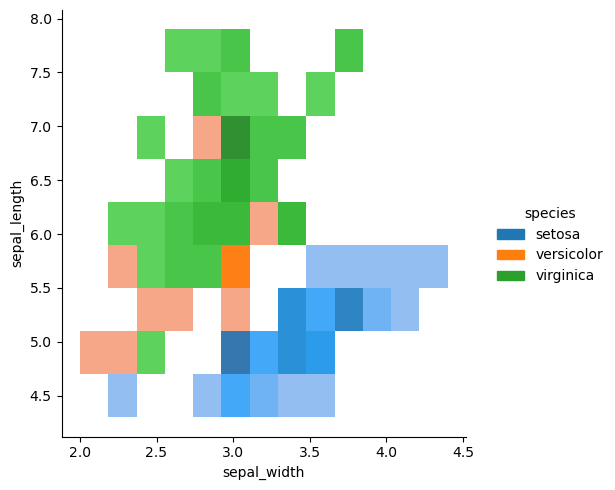
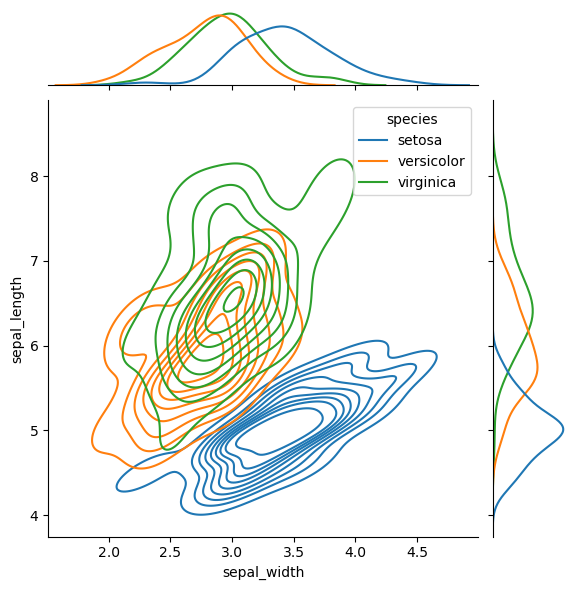
Sometimes it’s useful to see the marginal distributions

sns.jointplot(
    data=df,
    x='sepal_width', y='sepal_length', hue='species',
    kind="kde"
)

<seaborn.axisgrid.JointGrid at 0x14913d9614c0>

Interactive plotting with Plotly

So far we have seen static visualizations made with matplotlib and seaborn. Though you can create interactive plots with these tools, it is a lot of work.

Plotly is designed to be interactive out of the box.

# import the plotly express library
import plotly.express as px

px.scatter(df, x='sepal_width', y='sepal_length', color='species', height=500, width=700)

Plotly has many impressive features. For instance, we can easily add groups and margin plots:

px.scatter(df, x='sepal_width', y='sepal_length', color='species', height=500, width=700, marginal_x='box', marginal_y='box')

px.scatter(data_frame=df, x='sepal_length', y='sepal_width', facet_row='species', height=500, width=700)

We can modify the information available in the tooltip:

px.scatter(data_frame=df, x='sepal_length', y='sepal_width', facet_row='species', height=500, width=700,
          hover_data = ['petal_length', 'petal_width'])

We can even make density plots right in Plotly

 px.density_contour(df, x="sepal_width", y="sepal_length", color='species', height=500, width=700)

Animations

Plotly makes it very easy to create animations

df = px.data.gapminder()
fig = px.scatter(df, x="gdpPercap", y="lifeExp", animation_frame="year", animation_group="country",
           size="pop", color="continent", hover_name="country", facet_col="continent",
           log_x=True, size_max=45, range_x=[100,100000], range_y=[25,90])
fig.show()

Saving interactive plots

One of the great features of plotly is that you can save interactive features and run them in the browser.

To demonstrate we will save the above interactive plot. Try opening the resulting html file in your browser.

fig.write_html("animated_fig.html")