Small Language Models: an introduction to autoregressive language modeling#
This notebook was partly inspired by this blog post on character-level bigram models: https://medium.com/@fareedkhandev/create-gpt-from-scratch-using-python-part-1-bd89ccf6206a
import os
os.environ["TOKENIZERS_PARALLELISM"] = "false"
The language modeling task#
What is language modeling?#
In this notebook, we take a first look at the language modeling task. “Language Modeling” has two parts:
“Language” is what it sounds like. For our purposes, we will always represent language with text. We will also talk about
tokens: pieces of text. These could be words, word chunks, or individual characters.documents: a sequence of tokens about something. These could be individual tweets, legal contracts, love letters, emails, or journal abstracts.dataset: a collection of documents. We will be using a PubMed dataset containing 50 thousand abstracts.vocabulary: the set of all unique tokens in our dataset.
“Modeling” refers to creating a mathematical structure that, in some way, corresponds to observed data. In this case, the data is language, so the model should quantiatively capture something about the nature of language. We need to make this more concrete.
Language modeling as probabilistic modeling#
Let’s try to make the idea of mathematically modeling language more concrete. We will develop models for the vector of tokens that appear in a document. We denote this as $\( p(\langle w_i\rangle_{i=1}^{L}) \)\( where \)w_i\( is the token at position \)i\( in a document and \)L$ is the number of words in the document. The angle bracket with limits notation here denotes the vector of all tokens specified by the limits.
If we knew this joint distribution, we could sample new documents \(d\): $\( d \sim p(\langle w_i\rangle_{i=1}^{L}) \)\( This is called _language generation_ because \)d\( is not in the dataset that we used to learn \)p(\langle w_i\rangle_{i=1}^{L})$, but it “looks like” it is from that dataset.
Autoregressive language modeling#
Let’s make a simplifying assumption. Let’s assume that the probability for token \(i\) only depends on the previous tokens as shown in this figure (Notice: no arrows going from right to left.)
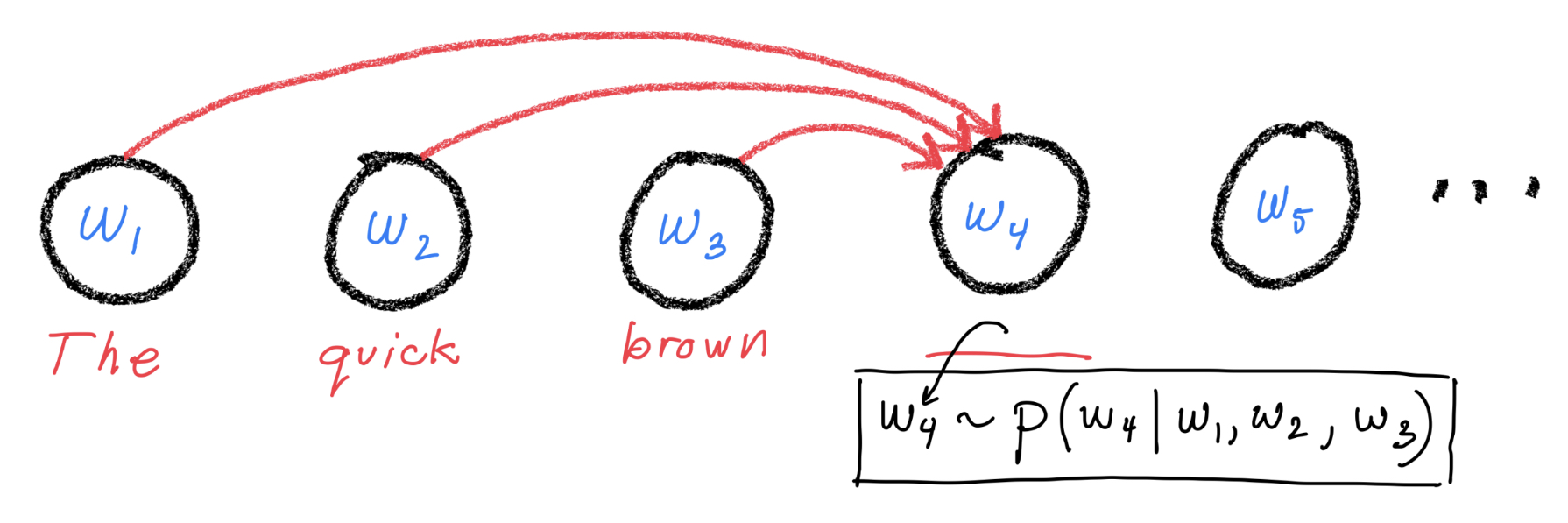
Mathematically, this can be expressed as: $\( p(w_i | \langle w_j\rangle_{j\neq i}) = p(w_i | \langle w_j\rangle_{j=1}^{i-1}) \)\( This gives us a natural way to sample documents because it implies that \)\( p(\langle w_i\rangle_{i=1}^{L}) = p(w_1)\prod_{j=2}^L p(w_j | \langle w_i\rangle_{i=1}^{j-1}) \)$ So, to generate a new document, we can
start with a prompt token or token sequence
sample the next token conditioned on the prompt and append it to the prompt
sample the next token conditioned on the appended prompt and append it to the appended prompt
and so on….
This is how ChatGPT works! This approach goes by the names autoregressive language modeling or causal language modeling.
This is not how all language modeling works. BERT, for instance, uses masked language modeling, where random tokens in a sequence are sampled by considering the tokens at all other positions. Word2Vec models tokens using a neighborhood of nearby tokens.
Also, we still haven’t said anything about how you actually write down the functional form of \(p(w_i | \langle w_j\rangle_{j=1}^{i-1})\). There are many possible architectures (an incomplete list in approximate historical ordering):
Markov model
1D CNN
RNN
LSTM/GRU
Transformer
We will spend the next notebook digging deep into the last option. Before we do, though, let’s try to get a better understanding of language models by looking closely at a simple Markov model.
~~Large~~ Small Language Model#
The simplest, non-trivial model#
Before we move on to attention, transformers, and LLMs, let’s first write down and fit a very simple language model for the PubMed dataset. This will provide a baseline for more sophisticated techniques and will give us a better understanding of how autoregressive language modeling works. Most of the lessons learned will transfer directly to the LLM case.
The simplest, non-trivial model comes from assuming that the distribution for token \(i\) only depends on token \(i-1\). Graphically:
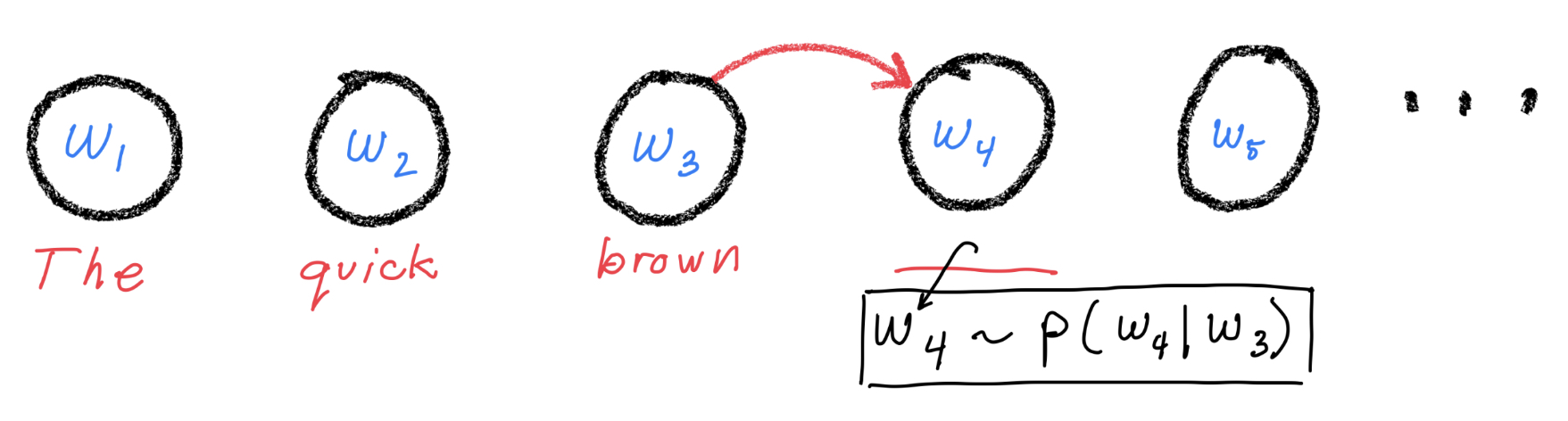
With this Markov assumption, the conditional distribution for token \(i\) simplifies to $\( p(w_i | \langle w_j\rangle_{j=1}^{i-1}) = p(w_i | w_{i-1}) \)$
The probability distribution for the entire sequence is then $\( p(\langle w_i\rangle_{i=1}^{L}) = p(w_{1})\prod_{i=2}^{L}p(w_{i}|{w}_{i-1}) \)$ allowing us to generate sequences as described above.
In what ways might this be an inadequate model for human language?
Estimating the model from data#
How can we estimate this model mathematically?
We start by observing that the model only depends on a set of probabilities describing the likelihood of one word given another word. These probabilities are called transition matrix elements, $\( T_{\alpha\beta} = p(w_i=\alpha | w_{i-1}=\beta)\\ \)\( where the matrix elements satisfy \)\( T_{\alpha\beta} \geq 0 \\ \sum_\alpha T_{\alpha\beta} =1 \)\( where \)\alpha\( and \)\beta\( are two tokens in our vocabulary. If the vocab size is \)V\(, the estimation task comes down to inferring the \)V\times V$ transition matrix elements describing the probability of going from any word to any other word.
Estimating with frequency tables#
One straightforward way to estimate these probabilities would be to list all of the neighbor pairs of tokens in our dataset and for each conditioning token \(\beta\) look at the share into each choice of \(\alpha\). This can be made to work, though we would have to deal with the fact that many token pairs will never appear.
Estimating with gradient descent#
In the code below, we will take a different approach. We will estimate the probabilities using a maximum likelihood based approach with gradient descent. For the Markov model, the two approaches are formally equivalent up to how they deal with the missing pairs. However, the gradient descent approach will generalize to more complicated models including transformer-based LLMs!
Enough talk#
Load our PubMed data#
Make sure you have the dataset.py in your working directory.
wget https://raw.githubusercontent.com/clemsonciti/rcde_workshops/master/pytorch_llm/dataset.py
# use the dataset.py file
from dataset import PubMedDataset
dataset = PubMedDataset("/project/rcde/datasets/pubmed/mesh_50k/splits/")
dl_train = dataset.get_dataloader('train', batch_size=3)
batch = next(iter(dl_train))
print(batch.keys())
next(iter(dl_train))
Build our small language model#
For the Markov model, we need to know the size of our vocabulary.
vocab_size = dataset.tokenizer.vocab_size
vocab_size
Yikes, that’s a big vocabulary! The size of the transition matrix will be vocab_size * vocab_size. Let’s estimate how much memory that would take to store:
# memory needed to store the transition matrix (in gigabytes)
vocab_size * vocab_size * 32 / 8 / 1e9
That’s huge, but let’s just try it anyway. Let’s write down our pytorch model. Just a little notation first:
\(N\): The batch size in batch gradient descent
\(L\), \(L_\mathrm{batch}\): The document sequence length or the sequence length of the batch, respectively.
\(V\): the size of our vocab
Without further ado, let’s write down the model:
import torch
import torch.nn.functional as F
class MarkovChain(torch.nn.Module):
def __init__(self, vocab_size):
super().__init__()
# the transition matrix logits
# nn.Embedding is just a matrix. Each input token will have a learnable
# parameter vector with one element for each output token.
# the transition matrix elements are computed by taking the softmax along the output dimension
self.t_logits = torch.nn.Embedding(vocab_size, vocab_size)
# let's start with the assumption that most transitions are very improbable
# large negative logit -> low probability
self.t_logits.weight.data -= 10.0
def forward(self, x):
logits = self.t_logits(x)
# logits.shape == (N, L_batch, V). Remember (batch size, sequence length, vocab size).
return logits # turns out we never actually need to compute the softmax for MLE
def numpars(self):
return sum(p.numel() for p in self.parameters() if p.requires_grad)
Let’s try it on some actual data to make sure it works.
model = MarkovChain(vocab_size)
print("Trainable params (millions):", model.numpars()/1e6)
model
y = model(batch["input_ids"])
y.shape
The output tensor has shape batch_size x sequence_length x vocab_size. We interpret these outputs as the logits of the next word. The probability of the next word is then
p_next_words = y.softmax(dim=-1)
# check that the total probability over possible next tokens sums to 1:
p_next_words.sum(dim=-1)
Generate text for untrained model#
def generate(model, idx, max_new_tokens):
"""
Recursively generate a sequence one token at a time
"""
# idx is (N, L) array of indices in the current context
for _ in range(max_new_tokens):
# get the predictions
with torch.no_grad():
logits = model(idx) # [N, L, V]
# trim last time step. It is prediction for token after end of sequence
logits = logits[:, -1] # becomes (N, V)
# apply softmax to get probabilities
probs = F.softmax(logits, dim=-1) # (N, V)
# sample from the distribution
idx_next = torch.multinomial(probs, num_samples=1) # (N, 1)
# append sampled index to the running sequence
idx = torch.cat((idx, idx_next), dim=1) # (N, L+1)
return idx
Let’s use our model to generate some sequences!
prompts = [
"We compared the prevalence of", # organ-specific autoantibodies in a group of Helicobacter..."
"We compared the prevalence of",
"We compared the prevalence of"
]
prompt_ids = dataset.tokenizer(prompts, return_tensors='pt')['input_ids']
prompt_ids
dataset.decode_batch(prompt_ids)
# trim off unwanted [SEP] tokens which act like our special end-of-sequence token.
prompt_ids = prompt_ids[:,:-1]
prompt_ids
# generate more ids
gen_ids = generate(model, prompt_ids, 15)
gen_ids
# decode into text
dataset.decode_batch(gen_ids)
Terrible! For now.
If we’re to improve it, we need an objective to optimize.
Loss function#
Remember, our goal is to learn good values for the transition matrix elements. We will do this by minimizing the cross entropy loss for next token prediction. This loss measures how likely the actual next tokens are under the predicted probability distribution over tokens.
It turns out, we never actually have to use the next token probabilities. This is because cross entropy only depends on log probabilities. So, rather than take exponentials of the logits, only to take the log again while computing cross entropy, we just stick with logits. Pytorch’s built-in cross entropy loss function expects this.
# remember what our batch of inputs abstracts looks like:
batch['input_ids'].shape
# cut the last prediction off because this corresponds to a token after the last token in the input sequence
# y.shape == (N, L_batch, V)
pred_logits = y[:, :-1].permute(0,2,1) # (N, V, L_batch) as needed for F.cross_entropy(.)
# cut the first word off the targets because we can't predict the distribution for the first word from the autoregressive model
targets = batch['input_ids'][:, 1:]
pred_logits.shape, targets.shape
Make sure these shapes make sense to you!
Use the built in pytorch function to compute cross entropy for each position in the sequence
from torch.nn import functional as F
# pytorch expects the intput to have shape `sequence_length x batch_size x vocab_size`
token_loss = F.cross_entropy(pred_logits, targets, reduction='none')
token_loss.shape
This is the loss for each token. But remember, some of those tokens are just padding to make the batch tensor rectangular. We shouldn’t count those.
We can use the attention_mask data structure output by our dataset to take care of this.
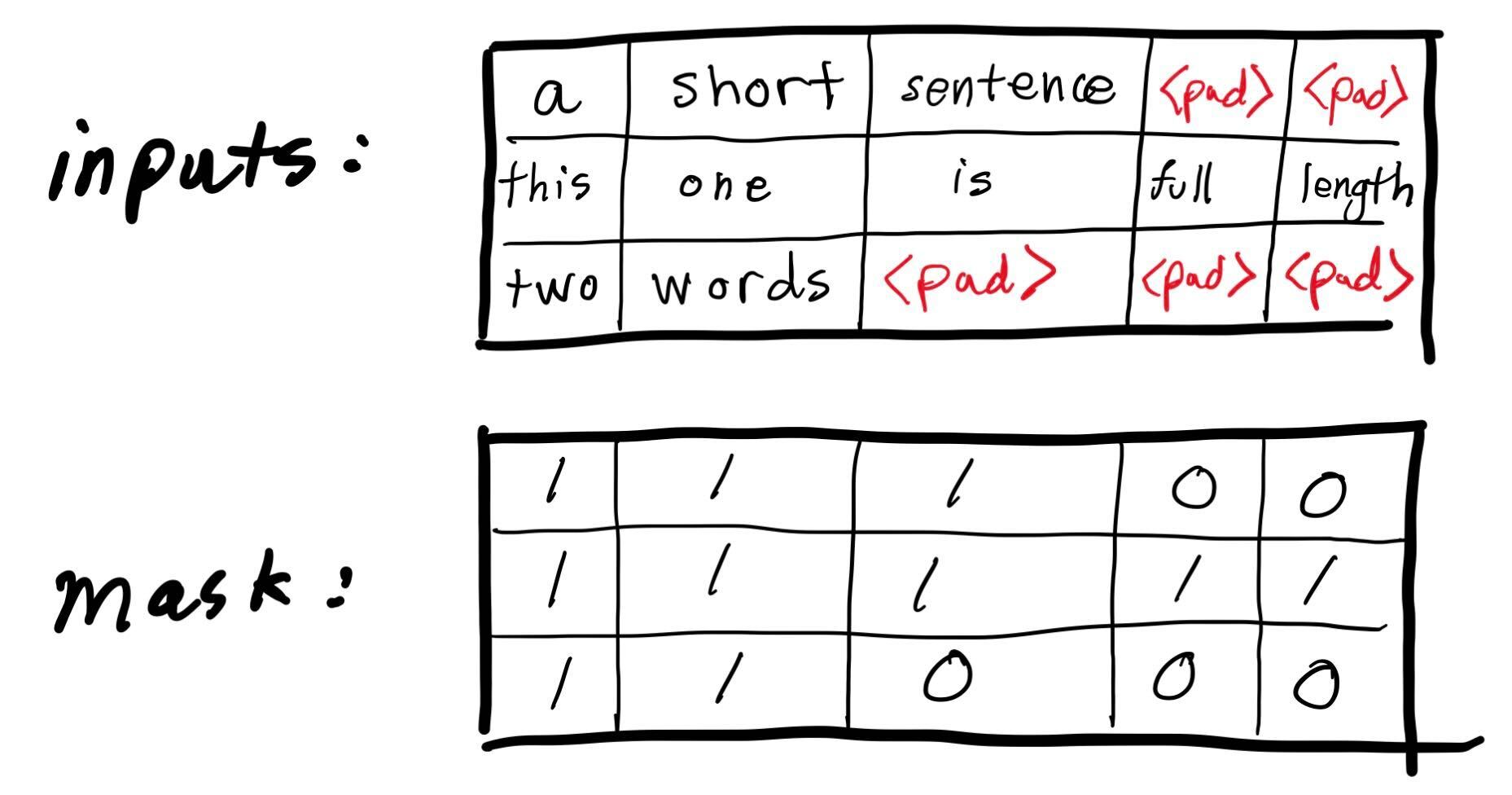
mask = batch['attention_mask'][:, 1:] # need to trim the first because our predictions are for tokens 2 through the end.
mask.shape, mask
We need to zero out the loss coming from the padding tokens and compute the average loss only counting the non-padding tokens.
Let’s put all of this logic into a function.
# let's put all this together in a custom loss function
def masked_cross_entropy(logits, targets, mask):
"""
Args:
- logits: The next token prediction logits. Last element removed. Shape (N, V, L-1)
- targets: Ids of the correct next tokens. First element removed (N, L-1)
- mask: the attention mask tensor. First element removed (N, L-1)
"""
token_loss = F.cross_entropy(logits, targets, reduction="none")
# total loss zeroing out the padding terms
total_loss = (token_loss * mask).sum()
# average per-token loss
num_real = mask.sum()
mean_loss = total_loss / num_real
return mean_loss
masked_cross_entropy(pred_logits, targets, mask)
Time to train the model!#
This is boilerplate pytorch optimization code, so we will zip over it. Pytorch’s documentation has a useful Beginner’s guide, here.
# training settings
batch_size=128
num_workers=20
num_epochs=2
learning_rate=0.1 # this model benefits from a large learning rate
# reinitialize dataset for good measure
dataset = PubMedDataset("/project/rcde/datasets/pubmed/mesh_50k/splits/")
# train/test dataloaders
dl_train = dataset.get_dataloader('train', batch_size=batch_size, num_workers=num_workers)
dl_test = dataset.get_dataloader('test', batch_size=batch_size, num_workers=num_workers)
# reinitialize the model on gpu
model = MarkovChain(vocab_size).to('cuda')
# create the pytorch optimizer
optimizer = torch.optim.AdamW(model.parameters(), lr=learning_rate)
# run the training loop
for epoch in range(num_epochs):
print(f"START EPOCH {epoch+1}")
for ix, batch in enumerate(dl_train):
x = batch["input_ids"][:,:-1].to('cuda') # remove last
targets = batch["input_ids"][:,1:].to('cuda') # remove first
mask = batch["attention_mask"][:,1:].to('cuda') # remove first
logits = model(x).permute(0,2,1)
loss = masked_cross_entropy(logits, targets, mask)
# do the gradient optimization stuff
optimizer.zero_grad()
loss.backward()
optimizer.step()
if ix % 20 ==0:
print(f"Batch {ix} training loss: {loss.item()}")
# test; did the learning generalize?
for ix, batch in enumerate(dl_test):
x = batch["input_ids"][:,:-1].to('cuda') # remove last
targets = batch["input_ids"][:,1:].to('cuda') # remove first
mask = batch["attention_mask"][:,1:].to('cuda') # remove first
with torch.no_grad():
logits = model(x).permute(0,2,1)
loss = masked_cross_entropy(logits, targets, mask)
if ix % 5 ==0:
print(f"Batch {ix} testing loss: {loss.item()}")
The learning seems to have generalized well.
# generate some more samples now that we've trained the model
gen_samples = generate(model, prompt_ids.to('cuda'), 30)
dataset.decode_batch(gen_samples)
The model is still terrible, though it has started to learn some very basic patterns.
Cleaning up#
We will reuse a lot this code in later sections of the workshop. I’ve pulled the import parts into utils.py. Copy the file into your working directory:
wget https://raw.githubusercontent.com/clemsonciti/rcde_workshops/master/pytorch_llm/utils.py
from utils import train, test, generate
train??
Low rank Markov Model#
With all the setup in place, it’s easy to start experimenting with different models. We saw how huge the embedding matrix was and we worried that this would lead to bad performance. One way to get around this is to create a low-rank version of the markov model.
import torch
import torch.nn.functional as F
class MarkovChainLowRank(torch.nn.Module):
def __init__(self, vocab_size, embed_dim):
super().__init__()
# We project down to size `embed_dim` then back up to `vocab_size`
# the total number of parameters is 2 * vocab_size * embed_dim which
# can be much smaller than embed_dim * embed_dim
self.t_logits = torch.nn.Sequential(
torch.nn.Embedding(vocab_size, embed_dim),
torch.nn.Dropout(0.1), # zero out some of the embedding vector elements randomly to prevent overfitting
torch.nn.Linear(embed_dim, vocab_size, bias=False)
)
# let's start with the assumption that most transitions are very improbable
# large negative logit -> low probability
self.t_logits[-1].weight.data -= 10.0
def forward(self, x):
logits = self.t_logits(x) # tensor of shape (N, L, V). Remember (batch size, sequence length, vocab size).
return logits # turns out we never actually need to compute the softmax for MLE
def numpars(self):
return sum(p.numel() for p in self.parameters() if p.requires_grad)
embedding_dim=256
learning_rate=0.001 # this model requires a more normal learning rate.
model = MarkovChainLowRank(vocab_size, embed_dim = embedding_dim)
print("Trainable params (millions):", model.numpars()/1e6)
model
# reinitialize dataset for good measure
dataset = PubMedDataset("/project/rcde/datasets/pubmed/mesh_50k/splits/")
# train/test dataloaders
dl_train = dataset.get_dataloader('train', batch_size=batch_size, num_workers=num_workers)
dl_test = dataset.get_dataloader('test', batch_size=batch_size, num_workers=num_workers)
# reinitialize the model on gpu
model = MarkovChainLowRank(vocab_size, embed_dim=embedding_dim).to('cuda')
# create the pytorch optimizer
optimizer = torch.optim.AdamW(model.parameters(), lr=learning_rate)
# train
for epoch in range(num_epochs):
print(f"START EPOCH {epoch+1}")
train(model, dl_train, optimizer, reporting_interval=20)
# test how well the model generalizes:
test(model, dl_test, reporting_interval=5)
The cross entropy is just a little worse. Let’s see about the generated samples:
# generate some more samples for the low-rank model
gen_samples = generate(model, prompt_ids.to('cuda'), 30)
dataset.decode_batch(gen_samples)
Still pretty terrible – maybe a bit worse than the full-rank model. But much more parameter efficieint.
Can you think of other ways to improve the model?
Conclusions#
Clearly, it isn’t enough to only condition on the previous token. We should condition on all previous tokens. That’s where transformers come in. Transformers will allow us to learn the full conditional distribution \(p(w_i | \langle w_j\rangle_{j=1}^{i-1})\) without making strong assumptions about the structure of the relationship between consecutive tokens.
Nevertheless, as we will see, the setup and training procedure for transformer-based LLMs will be almost identical to the what we used here for our small language model.
